题目内容
13.甲船在A处遇险,在甲船正西南10海里B处的乙船收到甲船的报警后,测得甲船是沿着方位角105°的方向,以每小时9海里的速度向某岛靠近.如果乙船要在40分钟内追上甲船,则乙船应以多少速度并沿什么方向航行?分析 通过画出图象,设乙船速度为ν海里/小时,在C处追上甲船,在△ABC中利用余弦定理可知ν=21,利用正弦定理可知sin∠B=$\frac{3\sqrt{3}}{14}$,进而计算可得结论.
解答 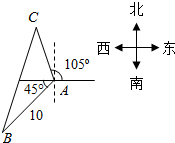 解:如图,设乙船速度为ν海里/小时,在C处追上甲船,
解:如图,设乙船速度为ν海里/小时,在C处追上甲船,
∠BAC=45°+180°-105°=120°,
在△ABC中,由余弦定理得:BC2=AC2+AB2-2AC•AB•cos∠BAC,
即$(\frac{2}{3}v)^{2}$=$(\frac{2}{3}×9)^{2}$+102-2×$\frac{2}{3}$×9×10×cos120°,
整理得:ν=21,
又由正弦定理可知:$\frac{BC}{sin∠BAC}$=$\frac{AC}{sin∠B}$,
∴sin∠B=$\frac{AC•sin∠BAC}{BC}$=$\frac{\frac{2}{3}×9}{\frac{2}{3}×21}$×sin∠120°=$\frac{3\sqrt{3}}{14}$,
∴B≈21°47′,
即乙船应按东偏北45°+21°47′=66°47′的角度、以21海里/小时的速度航行.
点评 本题考查解三角形的应用,考查数形结合能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
3.已知圆锥高为h,底面圆半径、锥高、母线长构成等比数列,则圆锥的侧面积是( )
| A. | $\frac{1}{3}π{h^2}$ | B. | $\frac{1}{2}π{h^2}$ | C. | πh2 | D. | 2πh2 |
8.方程1og0.5(x+1)+x2=2的解的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.已知在三棱锥P-ABC中,PA、PB、PC两两互相垂直,且PA=1,PB=$\sqrt{6}$,PC=3,则该三棱锥外接球的表面积为( )
| A. | 16π | B. | 64π | C. | $\frac{32π}{3}$ | D. | $\frac{252π}{3}$ |