题目内容
12.已知数列{an+1+an}的前n项和Sn=2n+1-2,a1=0.(1)求数列{an+1+an}的通项公式;
(2)求a2n.
分析 (1)当n≥2时bn=Sn-Sn-1=2n,当n=1时b1=2满足n≥2时bn的形式,即得结论;
(2)由an+1+an=bn=2n可得an+2+an+1=2n+1,两式相减得an+2-an=2n,利用拆项法将a2n写成a2+(a4-a2)+(a6-a4)+…+(a2n-2-a2n-4)+(a2n-a2n-2),计算即可.
解答 解:(1)设an+1+an=bn,
则n≥2时,bn=Sn-Sn-1=(2n+1-2)-(2n-2)=2n,
当n=1时,b1=S1=2,满足n≥2时bn的形式,
∴an+1+an=bn=2n;
(2)由(1)可知an+1+an=bn=2n,an+2+an+1=2n+1,
两式相减,得an+2-an=2n,
又∵a1=0,a1+a2=2,
∴a2=2,
∴a2n=a2+(a4-a2)+(a6-a4)+…+(a2n-2-a2n-4)+(a2n-a2n-2)
=2+22+24+…+22n-4+22n-2
=2+$\frac{{2}^{2}-{2}^{2n-2}•{2}^{2}}{1-{2}^{2}}$
=$\frac{{2}^{2n}}{3}+\frac{2}{3}$.
点评 本题考查求数列的通项、前n项和,利用拆项法是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
2.设F为抛物线y2=5x的焦点,P是抛物线上x轴上方的一点,若|PF|=3,则直线PF的斜率为( )
| A. | 3$\sqrt{3}$ | B. | $\sqrt{30}$ | C. | $\sqrt{35}$ | D. | 2$\sqrt{10}$ |
3.已知某个几何体的三视图如图所示,则这个几何体最长的棱长为( )
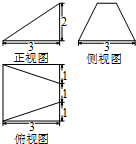

| A. | $\sqrt{14}$ | B. | $\sqrt{13}$ | C. | $\sqrt{10}$ | D. | 3 |
7.已知集合A={y|y=-x2+2,x∈R},B={y|y=-x+2,x∈R},则A∩B=( )
| A. | (-∞,2] | B. | {(0,2),(1,1)} | C. | {1,2} | D. | (0,2),(1,1) |
4. 如图,按英文字母表A、B、C、D、E、F、G、H、…的顺序有规律排列而成的鱼状图案中,字母“O”出现的个数为( )
如图,按英文字母表A、B、C、D、E、F、G、H、…的顺序有规律排列而成的鱼状图案中,字母“O”出现的个数为( )
 如图,按英文字母表A、B、C、D、E、F、G、H、…的顺序有规律排列而成的鱼状图案中,字母“O”出现的个数为( )
如图,按英文字母表A、B、C、D、E、F、G、H、…的顺序有规律排列而成的鱼状图案中,字母“O”出现的个数为( )| A. | 27 | B. | 29 | C. | 31 | D. | 33 |