题目内容
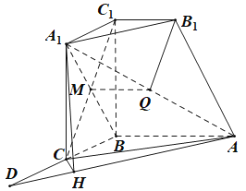
【题目】如图,在几何体![]() 中,平面
中,平面![]() ⊥底面
⊥底面![]() ,四边形
,四边形![]() 是正方形,
是正方形,![]() ,
,![]() 是
是![]() 的中点,且
的中点,且![]() ,
,![]()
(1)证明:![]() //平面
//平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)连接![]() ,
,![]() 交于
交于![]() 点,连接
点,连接![]() ,证明四边形
,证明四边形![]() 是平行四边形得到答案.
是平行四边形得到答案.
(2)过点![]() 作面
作面![]() 与面
与面![]() 的交线
的交线![]() ,交直线
,交直线![]() 于
于![]() ,证明
,证明![]() 即
即![]() 与面
与面![]() 所成的角,计算得到答案.
所成的角,计算得到答案.
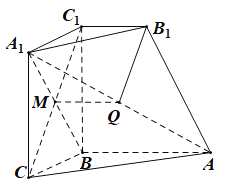
(1)证明:如图1所示,连接![]() ,
,![]() 交于
交于![]() 点,连接
点,连接![]() .
.
因为四边形![]() 是正方形,所以
是正方形,所以![]() 是
是![]() 的中点,
的中点,
又已知![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,
又因为![]() 且
且![]() ,所以
,所以![]() ,即四边形
,即四边形![]() 是平行四边形,
是平行四边形,
所以![]() ,因此
,因此![]() 平面
平面![]() .
.
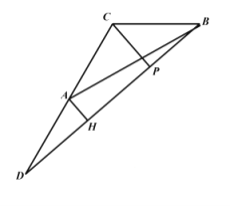
(2)如图2所示,过点![]() 作面
作面![]() 与面
与面![]() 的交线
的交线![]() ,交直线
,交直线![]() 于
于![]() .
.
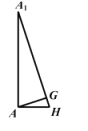
过![]() 作线
作线![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() .
.
再过![]() 作线
作线![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() 面
面![]() ,
,
所以![]() ,又因为
,又因为![]() ,
,
所以![]() ⊥面
⊥面![]() ,所以
,所以![]() 即
即![]() 与面
与面![]() 所成的角,
所成的角,
因为![]() 面
面![]() ,所以
,所以![]() ,
,
且![]() 为
为![]() 的中点,如图2所示,
的中点,如图2所示,![]() 为
为![]() 边上的高,
边上的高,
![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,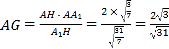 ,
,
所以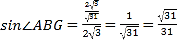 .
.

练习册系列答案
相关题目
【题目】某人准备投资1200万元办一所中学,为了考虑社会效益和经济效益,对该地区教育市场进行调查,得出一组数据,列表如下(以班级为单位).
市场调查表:
班级学生数 | 配备教师数 | 硬件建设费(万元) | 教师年薪(万元) | |
初中 | 50 | 2.0 | 28 | 1.2 |
高中 | 40 | 2.5 | 58 | 1.6 |
根据物价部门的有关规定:初中是义务教育阶段,收费标准适当控制,预计除书本费、办公费外,初中每人每年可收取600元.高中每人每年可收取1500元.因生源和环境等条件限制,办学规模以20至30个班为宜(含20个班与30个),教师实行聘任制.初、高中教育周期均为三年,设初中编制为![]() 个班,高中编制为
个班,高中编制为![]() 个班,请你合理地安排招生计划,使年利润最大.
个班,请你合理地安排招生计划,使年利润最大.

