Question

【题目】将圆为参数)上的每一点的横坐标保持不变，纵坐标变为原来的倍，得到曲线

(1)求出的普通方程；

(2)设直线： 与的交点为， ，以坐标原点为极点， 轴正半轴为极轴建立极坐标系，求过线段的中点且与垂直的直线的极坐标方程.

Answer 1

【答案】（1）（2）

【解析】试题分析：（1）本问首先应用伸缩变换公式，根据公式可以得到变化后的参数方程为（为参数），即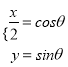，于是可以根据画为普通方程；（2）将曲线的普通方程与直线的方程联立，可以解方程组，方程组的解分别为两点坐标，于是可以求出直线的斜率及中点坐标，根据垂直关系可以求出线段的垂直平分线的方程，然后根据极坐标与直角坐标互化公式，即得到直线的极坐标方程.

试题解析：(1)设为圆上的任意一点，在已知的变换下变为上的点，

则有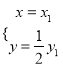

(2) 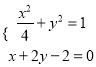解得：

所以则线段的中点坐标为，所求直线的斜率，于是所求直线方程为.

化为极坐标方程得： ，即