题目内容
已知 、
、 为双曲线C:
为双曲线C: 的左、右焦点,点
的左、右焦点,点 在曲线
在曲线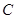 上,∠
上,∠ =
= ,则
,则 到
到 轴的距离为( )
轴的距离为( )
A. | B. | C. | D. |
B
解析试题分析:题中唯一的条件是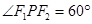 ,为了充分利用此条件,我们设
,为了充分利用此条件,我们设 ,且不妨设
,且不妨设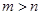 ,则根据双曲线定义有
,则根据双曲线定义有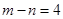 ,对
,对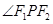 利用余弦定理有
利用余弦定理有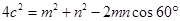 ,即
,即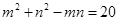 ,因此可求得
,因此可求得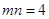 ,下面最简单的方法是利用面积法求得
,下面最简单的方法是利用面积法求得 到
到 轴的距离
轴的距离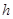 ,
,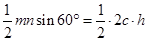 ,可得
,可得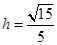 。
。
考点:双曲线的定义,余弦定理与三角形的面积。

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
椭圆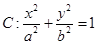
 的左、右焦点分别为
的左、右焦点分别为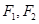 ,
,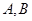 是
是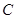 上两点,
上两点,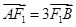 ,
, ,则椭圆
,则椭圆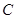 的离心率为( )
的离心率为( )
A.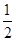 | B.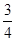 | C.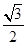 | D.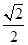 |
设 、
、 是曲线
是曲线 上的点,
上的点, ,则必有 ( )
,则必有 ( )
A. | B.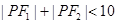 |
C. | D. |
椭圆 的焦距为( )
的焦距为( )
| A.10 | B.5 | C. | D. |
已知双曲线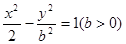 的左、右焦点分别是
的左、右焦点分别是 、
、 ,其一条渐近线方程为
,其一条渐近线方程为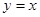 ,点
,点 在双曲线上.则
在双曲线上.则 ·
· = ( )
= ( )
| A.-12 | B.-2 | C. 0 | D.4 |
已知点 (3,4)在椭圆
(3,4)在椭圆 上,则以点
上,则以点 为顶点的椭圆的内接矩形
为顶点的椭圆的内接矩形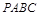 的面积是( )
的面积是( )
| A.12 | B.24 |
| C.48 | D.与 的值有关 的值有关 |
 ,0)、F2(
,0)、F2( 则该双曲线的方程是( )
则该双曲线的方程是( )



 +
+ =1的两焦点,过点F2的直线交椭圆于A,B两点.在△AF1B中,若有两边之和是10,则第三边的长度为 ( )
=1的两焦点,过点F2的直线交椭圆于A,B两点.在△AF1B中,若有两边之和是10,则第三边的长度为 ( )

