题目内容
若圆C与圆(x+2)2+(y-1)2=1关于原点对称,则圆C的方程是( ).
| A.(x-2)2+(y+1)2=1 | B.(x-2)2+(y-1)2=1 |
| C.(x-1)2+(y+2)2=1 | D.(x+1) 2+(y-2)2=1 |
A
解析试题分析:解:圆(x+2)2+(y-1)2=5的圆心A(-2,1),半径等于 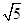 ,圆心A关于原点(0,0)对称的圆的圆心B(2,-1),故对称圆的方程为 (x-2)2+(y+1)2=5,故答案为 (x-2)2 +(y+1)2=5.故选A.
,圆心A关于原点(0,0)对称的圆的圆心B(2,-1),故对称圆的方程为 (x-2)2+(y+1)2=5,故答案为 (x-2)2 +(y+1)2=5.故选A.
考点:圆的方程
点评:本题考查求一个圆关于一个点的对称圆的方程的求法,求出圆心A关于原点(0,0)对称的圆的圆心B的坐标,是解题的关键.

练习册系列答案
相关题目
经过圆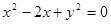 的圆心且与直线
的圆心且与直线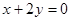 平行的直线方程是( )
平行的直线方程是( )
A.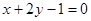 | B.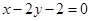 | C.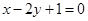 | D.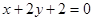 |
过圆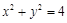 外一点
外一点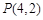 作圆的两条切线,切点分别为
作圆的两条切线,切点分别为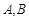 ,则
,则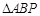 的外接圆方程是( )
的外接圆方程是( )
A.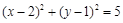 | B.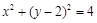 |
C.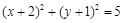 | D.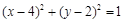 |
直线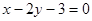 与圆
与圆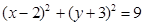 交于
交于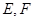 两点,则
两点,则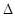
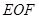 (
(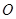 是原点)的面积为()
是原点)的面积为()
A.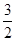 | B.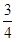 | C.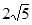 | D.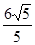 |
若方程 表示的曲线为圆,则
表示的曲线为圆,则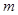 的取值范围是( )
的取值范围是( )
A. | B.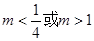 . . |
C.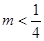 | D.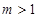 |
圆x2+y2+2x-4y=0的圆心坐标和半径分别是( )
| A.(1,-2),5 | B.(1,-2), |
| C.(-1,2),5 | D.(-1,2), |
直线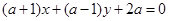 (
(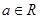 )与圆
)与圆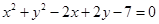 的位置关系是( )
的位置关系是( )
| A.相切 | B.相离 | C.相交 | D.不确定 |
以点(-5,4)为圆心,且与 轴相切的圆的方程是( )
轴相切的圆的方程是( )
A. | B. |
C.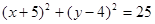 | D. |
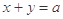 与圆
与圆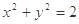 交于A、B两点,O是原点,若
交于A、B两点,O是原点,若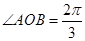 ,则
,则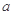 的值为( )
的值为( )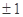 B.
B.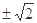 C.
C.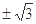 D.
D.