题目内容
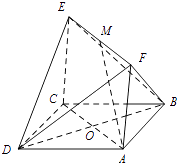
【题目】在正方体ABCD﹣A1B1C1D1中,动点P在底面ABCD内,且P到棱AD的距离与到面对角线BC1的距离相等,则点P的轨迹是( )
A.线段
B.椭圆的一部分
C.双曲线的一部分
D.抛物线的一部分
【答案】D
【解析】解:假设正方体边长为1,
作PM⊥AD、PE⊥BC、EF⊥BC1 , 连接PF,
因为PE⊥CC1 , BC∩CC1=C,所以PE⊥平面BCB1C1 ,
则PE⊥BC1 , 又EF⊥BC1 , PE∩EF=E,
所以BC1⊥平面PEF,则BC1⊥PF,
所以PF是P到对角线BC1的距离,
以D为原点,AD所在直线为x轴,DC所在直线为y轴建立直角坐标系;
设任意一点P(x,y),到直线AD距离为|y|,到BC的距离PE=1﹣y,
在RT△BEF中,BE=1﹣x,EF=![]() ,
,
在RT△PEF中,PF=![]()
因为P到棱AD的距离与到对角线BC1的距离相等,
所以|y|=![]() ,
,
化简得,(x﹣1)2=﹣4y+2(y![]() ),
),
所以点P的轨迹是抛物线的一部分,
故选:D.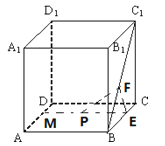
作PM⊥AD、PE⊥BC、EF⊥BC1 , 连接PF,由线面垂直的判定定理、定义可得:PF是P到BC1的距离,以D为原点,AD所在直线为x轴,DC所在直线为y轴建立直角坐标系,利用条件建立方程,化简后判断出点P的轨迹.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目