题目内容
 如图,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2
如图,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2| 2 |
(Ⅰ)证明:AM⊥PM;
(Ⅱ)求二面角P-AM-D的大小;
(Ⅲ)求点D到平面AMP的距离.
分析:(Ⅰ)取CD的中点E,连接PE、EM、EA,根据面面垂直的性质可知PE⊥平面ABCD,从而AM⊥PE,由勾股定理可求得AM⊥EM,又PE∩EM=E,满足线面垂直的判定定理则AM⊥平面PEM,根据线面垂直的性质可知AM⊥PM;
(Ⅱ)由(Ⅰ)可知EM⊥AM,PM⊥AM,根据二面角平面角的定义可知∠PME是二面角P-AM-D的平面角,然后在三角形PME中求出此角即可;
(Ⅲ)设D点到平面PAM的距离为d,连接DM,则根据等体积得VP-ADM=VD-PAM,建立关于d的等式解之即可得到点D到平面PAM的距离.
(Ⅱ)由(Ⅰ)可知EM⊥AM,PM⊥AM,根据二面角平面角的定义可知∠PME是二面角P-AM-D的平面角,然后在三角形PME中求出此角即可;
(Ⅲ)设D点到平面PAM的距离为d,连接DM,则根据等体积得VP-ADM=VD-PAM,建立关于d的等式解之即可得到点D到平面PAM的距离.
解答: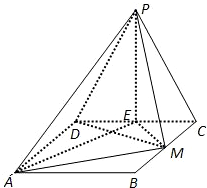 解:(Ⅰ)取CD的中点E,连接PE、EM、EA.
解:(Ⅰ)取CD的中点E,连接PE、EM、EA.
∵△PCD为正三角形,∴PE⊥CD,
∵平面PCD⊥平面ABCD,∴PE⊥平面ABCD
∴AM⊥PE(2分)
∵四边形ABCD是矩形
∴△ADE、△ECM、△ABM均为直角三角形
由勾股定理可求得:EM=
,AM=
,AE=3
∴EM2+AM2=AE2
∴AM⊥EM(4分)
又PE∩EM=E∴AM⊥平面PEM
∴AM⊥PM5分)
(Ⅱ)由(Ⅰ)可知EM⊥AM,PM⊥AM
∴∠PME是二面角P-AM-D的平面角(7分)
∴tan∠PME=
=
=1
∴∠PME=45°
∴二面角P-AM-D为45°((9分))
(Ⅲ)设D点到平面PAM的距离为d,连接DM,则
VP-ADM=VD-PAM,∴
S△ADM•PE=
S△PAM•d
而S△ADM=
AD•CD=2
在Rt△PEM中,由勾股定理可求得PM=
∴S△PAM=
AM•PM=3,所以:
×2
×
=
×3×d
∴d=
即点D到平面PAM的距离为
(13分)
 解:(Ⅰ)取CD的中点E,连接PE、EM、EA.
解:(Ⅰ)取CD的中点E,连接PE、EM、EA.∵△PCD为正三角形,∴PE⊥CD,
∵平面PCD⊥平面ABCD,∴PE⊥平面ABCD
∴AM⊥PE(2分)
∵四边形ABCD是矩形
∴△ADE、△ECM、△ABM均为直角三角形
由勾股定理可求得:EM=
| 3 |
| 6 |
∴EM2+AM2=AE2
∴AM⊥EM(4分)
又PE∩EM=E∴AM⊥平面PEM
∴AM⊥PM5分)
(Ⅱ)由(Ⅰ)可知EM⊥AM,PM⊥AM
∴∠PME是二面角P-AM-D的平面角(7分)
∴tan∠PME=
| PE |
| EM |
| ||
|
∴∠PME=45°
∴二面角P-AM-D为45°((9分))
(Ⅲ)设D点到平面PAM的距离为d,连接DM,则
VP-ADM=VD-PAM,∴
| 1 |
| 3 |
| 1 |
| 3 |
而S△ADM=
| 1 |
| 2 |
| 2 |
| 6 |
∴S△PAM=
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
∴d=
2
| ||
| 3 |
即点D到平面PAM的距离为
2
| ||
| 3 |
点评:本题主要考查了线面垂直的判定与性质,以及二面角的度量和点到平面的距离的求解,同时考查了空间想象能力和计算能力,转化与划归的思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=
如图,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC= (2010•朝阳区二模)如图,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2
(2010•朝阳区二模)如图,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2