题目内容
 (2010•朝阳区二模)如图,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2
(2010•朝阳区二模)如图,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2| 2 |
(Ⅰ)证明:AM⊥PM;
(Ⅱ)求二面角P-AM-D的大小;
(Ⅲ)求直线PD与平面PAM所成角的正弦值.
分析:法一:(Ⅰ)取DC的中点N,连接PN,AN,NM.因为PD=PC,所以PN⊥DC.因为PCD所在的平面垂直于矩形ABCD所在的平面,所以PN⊥平面ABCD.由此能够证明AM⊥PM.
(Ⅱ)由AM⊥PM且NM⊥AM,知∠PMN为二面角P-AM-D的平面角,由此能求出二面角P-AM-D的大小.
(Ⅲ)设点D到平面PAM的距离为d,由VP-AMD=VD-PAM,求得d=
,所以点D到平面PAM的距离为
.由此能求出直线PD与平面PAM所成角的正弦值.
法二:(Ⅰ)以D点为原点,分别以直线DA、DC为x轴、y轴,建立空间直角坐标系D-xyz,得D(0,0,0),P(0,1,
),C(0,2,0),A(2
,0,0),M(
,2,0),由
•
=0,得到AM⊥PM.
(Ⅱ)设
=(x,y,z),且
⊥平面PAM,由
,得
=(
,1,
),取
=(0,0,1),显然
⊥平面ABCD,由向量法能得到二面角P-AM-D的大小.
(Ⅲ) 设直线PD与平面PAM所成角为θ,由向量法能求出直线PD与平面PAM所成角的正弦值.
(Ⅱ)由AM⊥PM且NM⊥AM,知∠PMN为二面角P-AM-D的平面角,由此能求出二面角P-AM-D的大小.
(Ⅲ)设点D到平面PAM的距离为d,由VP-AMD=VD-PAM,求得d=
2
| ||
| 3 |
2
| ||
| 3 |
法二:(Ⅰ)以D点为原点,分别以直线DA、DC为x轴、y轴,建立空间直角坐标系D-xyz,得D(0,0,0),P(0,1,
| 3 |
| 2 |
| 2 |
| PM |
| PN |
(Ⅱ)设
| n |
| n |
|
| n |
| 2 |
| 3 |
| p |
| p |
(Ⅲ) 设直线PD与平面PAM所成角为θ,由向量法能求出直线PD与平面PAM所成角的正弦值.
解答: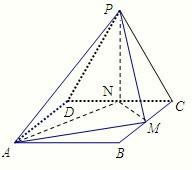 (方法一)
(方法一)
(Ⅰ)证明:取DC的中点N,连接PN,AN,NM.
因为PD=PC,所以PN⊥DC
又因为PCD所在的平面垂直于矩形ABCD所在的平面,
所以PN⊥平面ABCD,
所以PN⊥AM.因为AN=3,MN=
,AM=
,
所以NM⊥AM,
又因为PN∩NM=N,所以AM⊥PM.
(Ⅱ)由(Ⅰ)知,AM⊥PM且NM⊥AM,
所以∠PMN为二面角P-AM-D的平面角,
又因为PN=NM=
,
所以∠PMN=45°.即二面角P-AM-D的大小为45°.
(Ⅲ)设点D到平面PAM的距离为d,
因为VP-AMD=VD-PAM,
所以
•SAMD•PN=
SPAM•d,
求得d=
,即点D到平面PAM的距离为
.
设直线PD与平面PAM所成角为θ,
则sinθ=
=
,
故直线PD与平面PAM所成角的正弦值为
.
(方法二)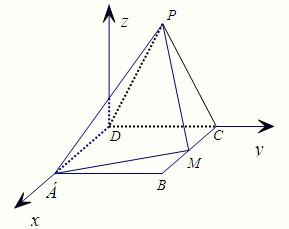 (Ⅰ) 证明 以D点为原点,分别以直线DA、DC为x轴、y轴,
(Ⅰ) 证明 以D点为原点,分别以直线DA、DC为x轴、y轴,
建立如图所示的空间直角坐标系D-xyz,
依题意,可得D(0,0,0),P(0,1,
),C(0,2,0),
A(2
,0,0),M(
,2,0),
∴
=(
,2,0)-(0,1,
)=(
,1,-
),
=(
,2,0)-(2
,0,0)=(-
,2,0),
∴
•
=-2+2+0=0,
即
⊥
,∴AM⊥PM.
(Ⅱ)解 设
=(x,y,z),
且
⊥平面PAM,
则
,
∴
,
=(
,1,
),
取
=(0,0,1),
显然
⊥平面ABCD,
∴cos<
,
>=
=
=
.
结合图形可知,二面角P-AM-D为45°.
(Ⅲ) 设直线PD与平面PAM所成角为θ,
则sinθ=|cos<
,
>|=|
|=
故直线PD与平面PAM所成角的正弦值为
.
 (方法一)
(方法一)(Ⅰ)证明:取DC的中点N,连接PN,AN,NM.
因为PD=PC,所以PN⊥DC
又因为PCD所在的平面垂直于矩形ABCD所在的平面,
所以PN⊥平面ABCD,
所以PN⊥AM.因为AN=3,MN=
| 3 |
| 6 |
所以NM⊥AM,
又因为PN∩NM=N,所以AM⊥PM.
(Ⅱ)由(Ⅰ)知,AM⊥PM且NM⊥AM,
所以∠PMN为二面角P-AM-D的平面角,
又因为PN=NM=
| 3 |
所以∠PMN=45°.即二面角P-AM-D的大小为45°.
(Ⅲ)设点D到平面PAM的距离为d,
因为VP-AMD=VD-PAM,
所以
| 1 |
| 3 |
| 1 |
| 3 |
求得d=
2
| ||
| 3 |
2
| ||
| 3 |
设直线PD与平面PAM所成角为θ,
则sinθ=
| d |
| PD |
| ||
| 3 |
故直线PD与平面PAM所成角的正弦值为
| ||
| 3 |
(方法二)
 (Ⅰ) 证明 以D点为原点,分别以直线DA、DC为x轴、y轴,
(Ⅰ) 证明 以D点为原点,分别以直线DA、DC为x轴、y轴,建立如图所示的空间直角坐标系D-xyz,
依题意,可得D(0,0,0),P(0,1,
| 3 |
A(2
| 2 |
| 2 |
∴
| PM |
| 2 |
| 3 |
| 2 |
| 3 |
| AM |
| 2 |
| 2 |
| 2 |
∴
| PM |
| PN |
即
| PM |
| AM |
(Ⅱ)解 设
| n |
且
| n |
则
|
∴
|
| n |
| 2 |
| 3 |
取
| p |
显然
| p |
∴cos<
| n |
| p |
| ||||
|
|
| ||
|
| ||
| 2 |
结合图形可知,二面角P-AM-D为45°.
(Ⅲ) 设直线PD与平面PAM所成角为θ,
则sinθ=|cos<
| DP |
| n |
| ||||
|
|
| ||
| 3 |
故直线PD与平面PAM所成角的正弦值为
| ||
| 3 |
点评:本题考查异面直线垂直的证明,求二面角的大小,求直线与平面所成角的正弦值.考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2010•朝阳区二模)为了测算如图阴影部分的面积,作一个边为6的正方形将其包含在内,并向正方形内随即投掷800个点,已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是
(2010•朝阳区二模)为了测算如图阴影部分的面积,作一个边为6的正方形将其包含在内,并向正方形内随即投掷800个点,已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是