题目内容
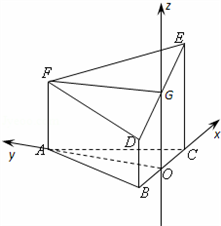
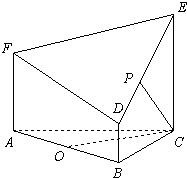
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥ 平面ABC,AB=2,AF=2,CE=3,BD=1,O为BC的中点.
(1)求证:AO∥平面DEF;
(2)求证:平面DEF⊥平面BCED;
(3)求平面DEF与平面ABC相交所成锐角二面角的余弦值.
(1)求证:AO∥平面DEF;
(2)求证:平面DEF⊥平面BCED;
(3)求平面DEF与平面ABC相交所成锐角二面角的余弦值.
证明:(1)取DE中点G,以BC中点O为原点,OC、OA分别为x、y轴,建系如图空间坐标系,则可得
A(0,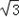 ,0)、B(﹣1,0,0)、C(1,0,0)、D(﹣1,0,1)、
,0)、B(﹣1,0,0)、C(1,0,0)、D(﹣1,0,1)、
E(1,0,3)、F(0,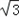 ,2)、G(0,0,2),
,2)、G(0,0,2),
∴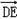 =(2,0,2),
=(2,0,2),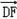 =(1,
=(1,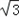 ,1).
,1).
设平面DEF的一法向量 =(x,y,z),则
=(x,y,z),则
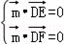 即
即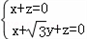 ,
,
取x=1,则y=0,z=﹣1,
可得 =(1,0,﹣1),
=(1,0,﹣1),
∵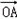 =(0,
=(0,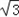 ,0),
,0),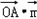 =0,
=0,
∴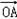 ⊥
⊥ .又OA
.又OA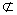 平面DEF,
平面DEF,
∴OA∥平面DEF.
(2)因为直线AO是平面BCDE的一条垂线,
∴平面BCED的一法向量为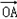 =(0,
=(0,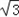 ,0),
,0),
∵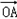
 =0,平面BCED的法向量与平面DEF的法向量互相垂直
=0,平面BCED的法向量与平面DEF的法向量互相垂直
∴平面DEF⊥平面BCED
(3)由(1)知平面DEF的一个法向量 =(1,0,﹣1),
=(1,0,﹣1),
平面ABC即xOy坐标平面,可得它的一个法向量 =(0,0,1),
=(0,0,1),
∵
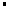
 =﹣1,
=﹣1, =
=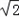 ,
,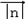 =1
=1
∴cos< ,
, >=
>=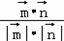 =﹣
=﹣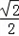
∴求平面DEF与平面ABC相交所成锐角二面角的余弦值为|cos< ,
, >|=
>|= .
.
A(0,
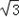 ,0)、B(﹣1,0,0)、C(1,0,0)、D(﹣1,0,1)、
,0)、B(﹣1,0,0)、C(1,0,0)、D(﹣1,0,1)、E(1,0,3)、F(0,
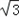 ,2)、G(0,0,2),
,2)、G(0,0,2),∴
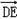 =(2,0,2),
=(2,0,2),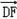 =(1,
=(1,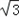 ,1).
,1).设平面DEF的一法向量
 =(x,y,z),则
=(x,y,z),则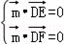 即
即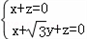 ,
,取x=1,则y=0,z=﹣1,
可得
 =(1,0,﹣1),
=(1,0,﹣1),∵
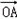 =(0,
=(0,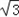 ,0),
,0),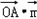 =0,
=0,∴
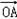 ⊥
⊥ .又OA
.又OA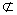 平面DEF,
平面DEF,∴OA∥平面DEF.
(2)因为直线AO是平面BCDE的一条垂线,
∴平面BCED的一法向量为
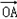 =(0,
=(0,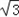 ,0),
,0),∵
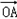
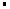
 =0,平面BCED的法向量与平面DEF的法向量互相垂直
=0,平面BCED的法向量与平面DEF的法向量互相垂直∴平面DEF⊥平面BCED
(3)由(1)知平面DEF的一个法向量
 =(1,0,﹣1),
=(1,0,﹣1),平面ABC即xOy坐标平面,可得它的一个法向量
 =(0,0,1),
=(0,0,1),∵

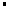
 =﹣1,
=﹣1, =
=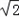 ,
,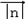 =1
=1∴cos<
 ,
, >=
>=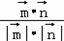 =﹣
=﹣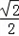
∴求平面DEF与平面ABC相交所成锐角二面角的余弦值为|cos<
 ,
, >|=
>|= .
.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,AB=2,BD=1,AF=2,CE=3,O为AB的中点.
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,AB=2,BD=1,AF=2,CE=3,O为AB的中点. 5、如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有( )
5、如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有( ) 如图所示的几何体是由以正三角形ABC为底面的直棱柱被平面 DEF所截而得.AB=2,BD=1,CE=3,AF=a,O为AB的中点.
如图所示的几何体是由以正三角形ABC为底面的直棱柱被平面 DEF所截而得.AB=2,BD=1,CE=3,AF=a,O为AB的中点. 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥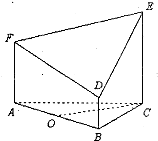 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,BD=1,AF=2,CE=3,O为AB的中点.
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,BD=1,AF=2,CE=3,O为AB的中点.