题目内容
 如图所示的几何体是由以正三角形ABC为底面的直棱柱被平面 DEF所截而得.AB=2,BD=1,CE=3,AF=a,O为AB的中点.
如图所示的几何体是由以正三角形ABC为底面的直棱柱被平面 DEF所截而得.AB=2,BD=1,CE=3,AF=a,O为AB的中点.(1)当a=4时,求平面DEF与平面ABC的夹角的余弦值;
(2)当a为何值时,在棱DE上存在点P,使CP⊥平面DEF?
分析:(1)通过建立空间直角坐标系,利用两平面的法向量的夹角即可得到二面角的余弦值;
(2)通过建立空间直角坐标系,利用线面垂直的判定定理即可得出.
(2)通过建立空间直角坐标系,利用线面垂直的判定定理即可得出.
解答:解:(1)分别取AB、DF的中点O、G,连接OC、OG.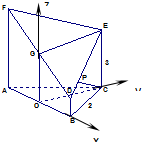
以直线OB、OC、OG分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,
∵AF=a=4,则D、E、F的坐标分别为D(1,0,1)、E(0,
,3)、F(-1,0,4),
∴
=(-1,
,2),
=(-2,0,3)
设平面DEF的法向量
=(x,y,z),
由
得
,
令z=6,则x=9,y=-
,∴
=(9,-
,6).
平面ABC的法向量可以取
=(0,0,1).
∴cos<
,
>=
=
=
.
∴平面DEF与平面ABC的夹角的余弦值为
.
(2)在(1)的坐标系中,AF=a,
=(-1,
,2),
=(-2,0,a-1),C(0,
,0).
因P在DE上,设
=λ
,
则
=
+
=(1,0,1)+λ(-1,
,2)=(1-λ,
λ,2λ+1).
∴
=
-
=(1-λ,
(λ-1),2λ+1).
于是CP⊥平面DEF的充要条件为
,得到
由此解得,λ=
,a=2.
即当a=2时,在DE上存在靠近D的第一个四等分点P,使CP⊥平面DEF.

以直线OB、OC、OG分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,
∵AF=a=4,则D、E、F的坐标分别为D(1,0,1)、E(0,
| 3 |
∴
| DE |
| 3 |
| DF |
设平面DEF的法向量
| n |
由
|
|
令z=6,则x=9,y=-
| 3 |
| n |
| 3 |
平面ABC的法向量可以取
| m |
∴cos<
| m |
| n |
| ||||
|
|
| 6 | ||||
|
| ||
| 10 |
∴平面DEF与平面ABC的夹角的余弦值为
| ||
| 10 |
(2)在(1)的坐标系中,AF=a,
| DE |
| 3 |
| DF |
| 3 |
因P在DE上,设
| DP |
| DE |
则
| OP |
| OD |
| DP |
| 3 |
| 3 |
∴
| CP |
| OP |
| OC |
| 3 |
于是CP⊥平面DEF的充要条件为
|
|
由此解得,λ=
| 1 |
| 4 |
即当a=2时,在DE上存在靠近D的第一个四等分点P,使CP⊥平面DEF.
点评:熟练掌握通过建立空间直角坐标系并利用两平面的法向量的夹角求二面角的余弦值、线面垂直的判定定理是解题的关键.

练习册系列答案
相关题目
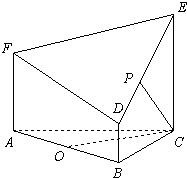 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,AB=2,BD=1,AF=2,CE=3,O为AB的中点.
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,AB=2,BD=1,AF=2,CE=3,O为AB的中点. 5、如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有( )
5、如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有( ) 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥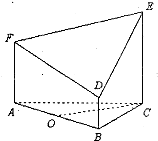 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,BD=1,AF=2,CE=3,O为AB的中点.
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,BD=1,AF=2,CE=3,O为AB的中点.