题目内容
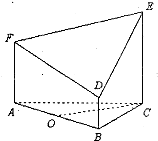 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,BD=1,AF=2,CE=3,O为AB的中点.
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,BD=1,AF=2,CE=3,O为AB的中点.(1)求证:OC⊥DF;
(2)试问线段CE上是否存在一点P,使得OP∥平面DEF?若存在,求出CP的长度,若不存在,请说明理由.
分析:(1)由ABC-FDE是由三棱柱所解得的几何体,知FA∥DB∥EC,且FA与DB确定平面ABDF,由FA⊥平面ABC,且OC?平面ABC,知FA⊥OC,由此能够证明OC⊥DF.
(2)取P为CE中点时,可使得OP∥平面DEF.再由题设条件,利用空间几何知识进行证明.
(2)取P为CE中点时,可使得OP∥平面DEF.再由题设条件,利用空间几何知识进行证明.
解答:(1)证明:∵ABC-FDE是由三棱柱所解得的几何体,
∴FA∥DB∥EC,且FA与DB确定平面ABDF,
∵FA⊥平面ABC,且OC?平面ABC,∴FA⊥OC,
∵△ABC是等边三角形,且O为AB中点,
∴OC是等边△ABC中AB边上的中线,
∴AB⊥OC,
∵FA?平面ABDF,AB?平面ABDF,且FA∩AB=A,
∴OC⊥平面ABDF,
∵DF?平面ABDF,∴OC⊥DF.
(2)解:线段CE上是存在一点P,使得OP∥平面DEF.取P为CE中点时,可使得OP∥平面DEF.
证明:取P为CE中点,O′为DF中点,连接OO′,OP,O′E(如图),
由(1)知FA∥DB∥EC,且FA≠DB,
∴四边形ABDF为梯形,
∵O,O′分别是两腰AB、DF的中点,
所以OO′是梯形BDFA的中位线,
所以OO′∥FA,且OO′=
(FA+DB),
∵FA=2,BD=1,∴OO’=
.
∵P是EC中点,所以CP=PE=
,
∵FA∥EC,∴OO′∥EP,且OO′=EP,
∴OO′EP是平行四边形,∴O′E∥OP,
∵O′E?DEF,OP?面DEF,
∴OP∥面DEF,
∴P为CE中点,使得OP∥平面DEF,此时CP=
.
∴FA∥DB∥EC,且FA与DB确定平面ABDF,
∵FA⊥平面ABC,且OC?平面ABC,∴FA⊥OC,
∵△ABC是等边三角形,且O为AB中点,
∴OC是等边△ABC中AB边上的中线,
∴AB⊥OC,
∵FA?平面ABDF,AB?平面ABDF,且FA∩AB=A,
∴OC⊥平面ABDF,
∵DF?平面ABDF,∴OC⊥DF.
(2)解:线段CE上是存在一点P,使得OP∥平面DEF.取P为CE中点时,可使得OP∥平面DEF.
证明:取P为CE中点,O′为DF中点,连接OO′,OP,O′E(如图),
由(1)知FA∥DB∥EC,且FA≠DB,
∴四边形ABDF为梯形,
∵O,O′分别是两腰AB、DF的中点,
所以OO′是梯形BDFA的中位线,
所以OO′∥FA,且OO′=
| 1 |
| 2 |
∵FA=2,BD=1,∴OO’=
| 3 |
| 2 |
∵P是EC中点,所以CP=PE=
| 3 |
| 2 |
∵FA∥EC,∴OO′∥EP,且OO′=EP,
∴OO′EP是平行四边形,∴O′E∥OP,
∵O′E?DEF,OP?面DEF,
∴OP∥面DEF,
∴P为CE中点,使得OP∥平面DEF,此时CP=
| 3 |
| 2 |
点评:本题考查与异面直线的证明,探索线段点的存在性.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.解题时要注意空间想象力的培养.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
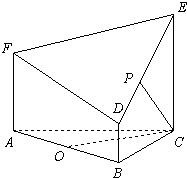 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,AB=2,BD=1,AF=2,CE=3,O为AB的中点.
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,AB=2,BD=1,AF=2,CE=3,O为AB的中点. 5、如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有( )
5、如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有( ) 如图所示的几何体是由以正三角形ABC为底面的直棱柱被平面 DEF所截而得.AB=2,BD=1,CE=3,AF=a,O为AB的中点.
如图所示的几何体是由以正三角形ABC为底面的直棱柱被平面 DEF所截而得.AB=2,BD=1,CE=3,AF=a,O为AB的中点. 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥