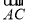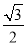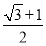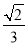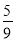题目内容
设P为椭圆 =1上的一点,F1,F2分别是该椭圆的左、右焦点,若|PF1|∶|PF2|=2∶1,则△PF1F2的面积为( ).
=1上的一点,F1,F2分别是该椭圆的左、右焦点,若|PF1|∶|PF2|=2∶1,则△PF1F2的面积为( ).
A.2 B.3 C.4 D.5
C
【解析】设P(x,y),则由已知易知F1(-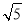 ,0),F2(
,0),F2(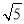 ,0).∵|PF1|∶|PF2|=2∶1,且|PF1|+|PF2|=6,∴|PF1|=4,|PF2|=2,即
,0).∵|PF1|∶|PF2|=2∶1,且|PF1|+|PF2|=6,∴|PF1|=4,|PF2|=2,即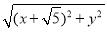 =4,
=4,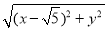 =2,两式联立可解得
=2,两式联立可解得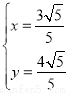 得P
得P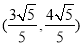 ,∴△PF1F2的面积为
,∴△PF1F2的面积为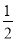 |F2F1|·|y|=
|F2F1|·|y|=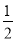 ×2
×2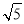 ×
×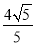 =4.
=4.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目