题目内容
10.若函数f(x)=a+|x|+log2(x2+2)有且只有一个零点,则实数a的值是( )| A. | -2 | B. | -1 | C. | 0 | D. | 2 |
分析 函数f(x)=a+|x|+log2(x2+2)有且只有一个零点可化为方程|x|+log2(x2+2)=-a有且只有一个根,令F(x)=|x|+log2(x2+2),可判断F(x)是偶函数,F(x)≥F(0)=1,从而可得a=-1.
解答 解:函数f(x)=a+|x|+log2(x2+2)有且只有一个零点可化为
方程|x|+log2(x2+2)=-a有且只有一个根,
令F(x)=|x|+log2(x2+2),
则F(x)是偶函数,且F(x)在[0,+∞)上是增函数,
故F(x)≥F(0)=1;
故方程|x|+log2(x2+2)=-a有且只有一个根时,
-a=1;
故a=-1.
故选B.
点评 本题考查了函数的零点与方程的根的联系与应用,同时考查了函数的性质的判断,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.若集合M={x|x2>4},N={x|1<x≤3},则N∩(∁RM)=( )
| A. | {x|1<x≤2} | B. | {x|-2≤x≤2} | C. | {x|-2≤x<1} | D. | {x|-2≤x≤3} |
18.设△ABC的内角A,B,C所对的边a,b,c成等比数列,则$\frac{sinA+cosA•tanC}{sinB+cosB•tanC}$的取值范围是( )
| A. | (0,+∞) | B. | $({\frac{{\sqrt{5}-1}}{2},+∞})$ | C. | $({0,\frac{{\sqrt{5}+1}}{2}})$ | D. | $({\frac{{\sqrt{5}-1}}{2},\frac{{\sqrt{5}+1}}{2}})$ |
19.已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$的左、右焦点,P为双曲线C右支上一点,且PF2⊥F1F2,PF1与y轴交于点Q,点M满足$\overrightarrow{{F}_{1}M}$=3$\overrightarrow{M{F}_{2}}$,若MQ⊥PF1,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{2}+\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}+\sqrt{6}}{2}$ |
 与函数
与函数 的图象分别交于点
的图象分别交于点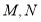 ,则当
,则当 达到最小时
达到最小时 的值为( )
的值为( )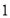 B.
B.
 D.
D.