题目内容
20.已知数列{an}中,a1=$\frac{1}{2}$,an+1=$\frac{1}{2}$an,正项数列{bn}的前n项的和为Sn,且对任意n∈N*,Sn是bn2和bn的等差中项.(1)求数列{an}与{bn}的通项公式;
(2)令cn=an•bn,数列{cn}的前n项的和为Tn,求证:$\frac{1}{2}$≤Tn<2.
分析 (1)a1=$\frac{1}{2}$,an+1=$\frac{1}{2}$an,可得:数列{an}是等比数列,利用等比数列的通项公式可得an.由对任意n∈N*,Sn是bn2和bn的等差中项.可得2Sn=${b}_{n}^{2}$+bn,利用递推公式可得:(bn+bn-1)(bn-bn-1)=0,由bn+bn-1>0,可得bn-bn-1=1,利用等差数列的通项公式可得:bn.
(2)由(1)可得:${c}_{n}=\frac{n}{{2}^{n}}$,Tn=$\frac{1}{2}+\frac{2}{{2}^{2}}$+$\frac{3}{{2}^{3}}$+…+$\frac{n}{{2}^{n}}$,利用“错位相减法”可得Tn,再利用Tn单调性,即可证明.
解答 (1)解:∵a1=$\frac{1}{2}$,an+1=$\frac{1}{2}$an,
∴数列{an}是等比数列,首项为$\frac{1}{2}$,公比为$\frac{1}{2}$,
∴${a}_{n}=(\frac{1}{2})^{n}$.
∵对任意n∈N*,Sn是bn2和bn的等差中项.
∴2Sn=${b}_{n}^{2}$+bn,
当n=1时,$2{b}_{1}={b}_{1}^{2}+{b}_{1}$,b1>0,解得b1=1.
当n≥2时,$2{S}_{n-1}={b}_{n-1}^{2}+{b}_{n-1}$,
∴2bn=${b}_{n}^{2}-{b}_{n-1}^{2}+{b}_{n}-{b}_{n-1}$,
∴(bn+bn-1)(bn-bn-1)=0,
∵bn+bn-1>0,
∴bn-bn-1=1,
∴数列{bn}为等差数列,首项为1,公差为1的等差数列,
∴bn=1+n-1=n.
(2)证明:由(1)可得:${c}_{n}=\frac{n}{{2}^{n}}$,
∴Tn=$\frac{1}{2}+\frac{2}{{2}^{2}}$+$\frac{3}{{2}^{3}}$+…+$\frac{n}{{2}^{n}}$,
$\frac{1}{2}{T}_{n}$=$\frac{1}{{2}^{2}}+\frac{2}{{2}^{3}}$+$\frac{3}{{2}^{4}}$+…+$\frac{n-1}{{2}^{n}}+\frac{n}{{2}^{n+1}}$,
∴$\frac{1}{2}{T}_{n}$=$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}-\frac{n}{{2}^{n+1}}$=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$-$\frac{n}{{2}^{n+1}}$=1-$\frac{2+n}{{2}^{n+1}}$,
∴Tn=2-$\frac{2+n}{{2}^{n}}$,
∵$\frac{2+n}{{2}^{n}}$>0,
∴Tn<2.
∵数列$\{\frac{2+n}{{2}^{n}}\}$单调递减,∴Tn单调递增,
∴Tn≥T1=$2-\frac{3}{2}$=$\frac{1}{2}$,
∴$\frac{1}{2}$≤Tn<2.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、递推式的应用、数列的单调性、“错位相减法”,考查了推理能力与计算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{6}$ | C. | 3 | D. | 2$\sqrt{3}$ |
| A. | -2 | B. | -1 | C. | 0 | D. | 2 |
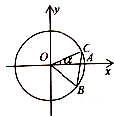 如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为$\frac{5}{13}$.
如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为$\frac{5}{13}$.