题目内容
19.已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$的左、右焦点,P为双曲线C右支上一点,且PF2⊥F1F2,PF1与y轴交于点Q,点M满足$\overrightarrow{{F}_{1}M}$=3$\overrightarrow{M{F}_{2}}$,若MQ⊥PF1,则双曲线C的离心率为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{2}+\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}+\sqrt{6}}{2}$ |
分析 如图所示,由PF2⊥F1F2,可得P$(c,\frac{{b}^{2}}{a})$,可得直线PF1的方程,即可得出Q.利用点M满足$\overrightarrow{{F}_{1}M}$=3$\overrightarrow{M{F}_{2}}$,可得M,由MQ⊥PF1,利用$\overrightarrow{MQ}•\overrightarrow{P{F}_{1}}$=0,化简解出即可.
解答  解:如图所示,
解:如图所示,
∵PF2⊥F1F2,
∴P$(c,\frac{{b}^{2}}{a})$,
∴直线PF1的方程为:$y=\frac{\frac{{b}^{2}}{a}-0}{c-(-c)}(x+c)$,
令x=0,可得y=$\frac{{b}^{2}}{2a}$,∴Q$(0,\frac{{b}^{2}}{2a})$.
∵点M满足$\overrightarrow{{F}_{1}M}$=3$\overrightarrow{M{F}_{2}}$,
∴$\overrightarrow{{F}_{1}M}=\frac{3}{4}\overrightarrow{{F}_{1}{F}_{2}}$,
∴$\overrightarrow{OM}$=$\overrightarrow{O{F}_{1}}$+$\frac{3}{4}\overrightarrow{{F}_{1}{F}_{2}}$=$(\frac{c}{2},0)$.
∵MQ⊥PF1,
∴$\overrightarrow{MQ}•\overrightarrow{P{F}_{1}}$=$(-\frac{c}{2},\frac{{b}^{2}}{2a})$•$(-2c,-\frac{{b}^{2}}{a})$=${c}^{2}-\frac{{b}^{4}}{2{a}^{2}}$=0,
∴2a2c2=(c2-a2)2,
化为e4-4e2+1=0,e>1,
解得${e}^{2}=2+\sqrt{3}$,
∴$e=\frac{\sqrt{6}+\sqrt{2}}{2}$.
故选:D.
点评 本题考查了双曲线的标准方程及其性质、向量垂直与数量积的关系,考查了推理能力与计算能力,属于中档题.

| A. | -2 | B. | -1 | C. | 0 | D. | 2 |
| A. | 2枝玫瑰的价格高 | B. | 3枝康乃馨的价格高 | ||
| C. | 价格相同 | D. | 不确定 |
| A. | (-∞,-$\sqrt{2}$)∪[$\sqrt{2}$,+∞) | B. | [-2,2] | C. | [-2,-$\sqrt{2}$]∪[$\sqrt{2}$,2] | D. | [-$\sqrt{2}$,$\sqrt{2}$] |
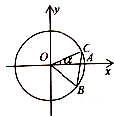 如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为$\frac{5}{13}$.
如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为$\frac{5}{13}$.