题目内容
5.已知直线l1:ax+2y+6=0,l2:x+(a-1)y+a2-1=0,若l1⊥l2,则a=$\frac{2}{3}$,若l1∥l2,则l1与l2的距离为$\frac{6\sqrt{5}}{5}$.分析 利用两条直线平行与垂直的充要条件即可得出.
解答 解:①当a=1时不满足条件,当a≠1时,∵l1⊥l2,∴$-\frac{a}{2}×(-\frac{1}{a-1})$=-1,解得a=$\frac{2}{3}$.
②∵l1∥l2,∴$-\frac{a}{2}=-\frac{1}{a-1}$,解得a=2或-1,a=2时两条直线重合,舍去.
∴a=-1,两条直线分别化为:x-2y-6=0,x-2y=0,
∴l1与l2的距离为=$\frac{|-6|}{\sqrt{5}}$=$\frac{6\sqrt{5}}{5}$.
故答案分别为:$\frac{2}{3}$,$\frac{6\sqrt{5}}{5}$.
点评 本题考查了两条直线平行与垂直的充要条件、斜率的计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
13.直线y=ax+b通过第一、二、三象限,则圆(x+a)2+(y+b)2=r2(r>0)的圆心位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.若函数f(x)=a+|x|+log2(x2+2)有且只有一个零点,则实数a的值是( )
| A. | -2 | B. | -1 | C. | 0 | D. | 2 |
17.已知集合A=|x|x>1|,B=|xy=$\sqrt{9-{x}^{2}}$|.那么A∩B=( )
| A. | [-3,3] | B. | (-1,3] | C. | (1,3] | D. | (1,3) |
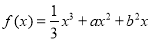 ,若
,若 是从
是从 三个数中任取的一个数,
三个数中任取的一个数, 是从
是从 三个数中任取的一个数,则使函数
三个数中任取的一个数,则使函数 有极值点的概率为_______.
有极值点的概率为_______.