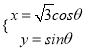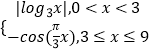题目内容
【题目】使函数y=sin（2x+θ）+ 
cos（2x+θ）为奇函数，且在[0， 
]上是减函数的θ一个值为（ ）
A.
B.
C.
D.
【答案】B
【解析】解：∵函数 
=2sin（2x+θ+ 
） 是奇函数， 故θ+ =kπ，k∈Z，θ=kπ﹣ ，故排除C．
若θ= ，f（x）=2sin（2x+ 
），不满足f（x）为奇函数，故排除A．
若θ= ，f（x）=2sin（2x+π）=﹣2sin2x是奇函数；在[0， 
]上，2x∈[0， 
]，
满足f（x）在[0， ]上是减函数，故B满足条件．
若θ= 
，f（x）=2sin（2x+2π）=2sin2x是奇函数；在[0， ]上，2x∈[0， ]，
f（x）在[0， ]上是增函数，不满足在[0， ]上是减函数，故排除D，
故选：B．
【考点精析】解答此题的关键在于理解正弦函数的奇偶性的相关知识，掌握正弦函数为奇函数，以及对正弦函数的单调性的理解，了解正弦函数的单调性：在
上是增函数；在
上是减函数．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
