Question

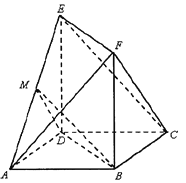
【题目】（题文）如图，在多面体中， 是正方形， 平面, 平面, ,点为棱的中点.

（1）求证：平面平面；

（2）若,求三棱锥的体积.

Answer 1

【答案】(1)见解析；（2）三棱锥的体积为.

【解析】试题分析：

（1）设与交于点，则为的中点，由三角形中位线的性质可得平面，由面面垂直的性质定理可得，则平面.最后利用面面平行的判断定理可得平面平面.

（2）连接.由几何关系可证得AC⊥平面，且垂足为， 则.

试题解析：

（1）证明：设与交于点，则为的中点，

∴.

∵平面， 平面，

∴平面.

∵平面， 平面，且，

∴，

∴为平行四边形，∴.

∵平面， 平面，

∴平面.

又∵，

∴平面平面.

（2）连接.在正方形中， ，

又∵平面，∴.

∵,

∴AC⊥平面，且垂足为，

∴,

∴三棱锥的体积为.