题目内容
已知数列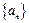
 中,
中,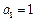 ,
,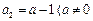 且
且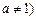 ,其前
,其前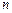 项和为
项和为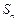 ,且当
,且当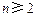 时,
时,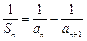 .
.
⑴求证:数列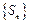 是等比数列;
是等比数列;
⑵求数列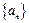 的通项公式;
的通项公式;
⑶若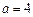 ,令
,令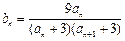 ,记数列
,记数列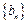 的前
的前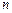 项和为
项和为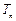 .设
.设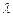
 是整数,问是否存在正整数
是整数,问是否存在正整数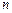 ,使等式
,使等式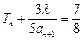 成立?若存在,求出
成立?若存在,求出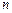 和相应的
和相应的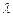 值;若不存在,请说明理由.
值;若不存在,请说明理由.
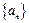
 中,
中,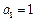 ,
,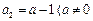 且
且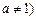 ,其前
,其前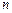 项和为
项和为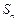 ,且当
,且当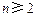 时,
时,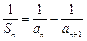 .
.⑴求证:数列
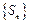 是等比数列;
是等比数列;⑵求数列
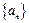 的通项公式;
的通项公式;⑶若
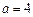 ,令
,令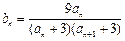 ,记数列
,记数列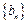 的前
的前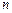 项和为
项和为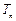 .设
.设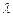
 是整数,问是否存在正整数
是整数,问是否存在正整数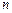 ,使等式
,使等式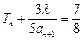 成立?若存在,求出
成立?若存在,求出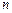 和相应的
和相应的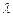 值;若不存在,请说明理由.
值;若不存在,请说明理由.(1)证明见解析
(2)
(3)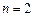
(2)

(3)
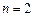
⑴当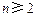 时,
时,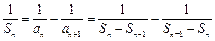 ,
,
化简得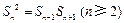 ,
,
又由 ,可推知对一切正整数
,可推知对一切正整数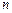 均有
均有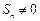 ,
,
∴数列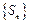 是等比数列. ---------------- 4分
是等比数列. ---------------- 4分
⑵由⑴知等比数列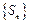 的首项为1,公比为
的首项为1,公比为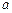 , ∴
, ∴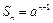 .
.
当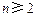 时,
时,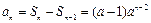 ,又
,又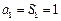 ,
,
∴ ----------8分
----------8分
⑶当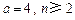 时,
时,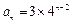 ,此时
,此时
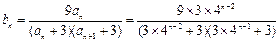
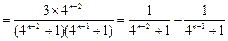 ,
,
又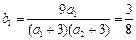 ,
,
∴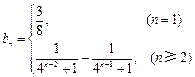
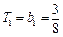 ,
,
当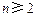 时,
时,
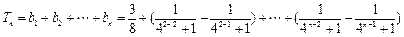
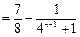 .
.
若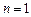 ,则等式
,则等式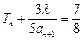 为
为 ,
,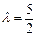 不是整数,不符合题意.
不是整数,不符合题意.
若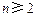 ,则等式
,则等式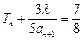 为
为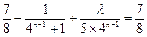 ,
,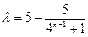
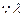 是整数,∴
是整数,∴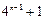 是5的因数.
是5的因数.
∴当且仅当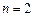 时,
时,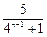 是整数, ∴
是整数, ∴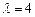
综上所 述,当且仅当
述,当且仅当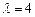 时,存在正整数
时,存在正整数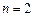 ,使等式
,使等式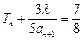 成立.
成立.
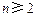 时,
时,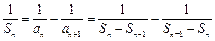 ,
,化简得
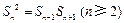 ,
,又由
 ,可推知对一切正整数
,可推知对一切正整数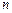 均有
均有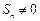 ,
,∴数列
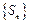 是等比数列. ---------------- 4分
是等比数列. ---------------- 4分⑵由⑴知等比数列
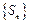 的首项为1,公比为
的首项为1,公比为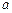 , ∴
, ∴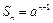 .
.当
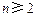 时,
时,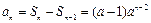 ,又
,又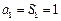 ,
,∴
 ----------8分
----------8分⑶当
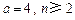 时,
时,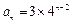 ,此时
,此时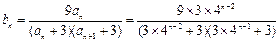
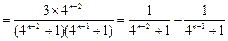 ,
,又
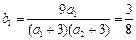 ,
,∴
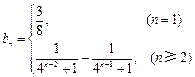
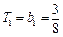 ,
,当
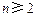 时,
时,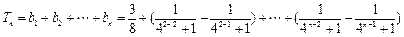
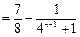 .
.若
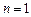 ,则等式
,则等式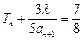 为
为 ,
,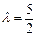 不是整数,不符合题意.
不是整数,不符合题意.若
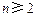 ,则等式
,则等式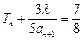 为
为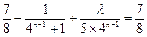 ,
,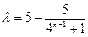
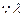 是整数,∴
是整数,∴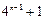 是5的因数.
是5的因数.∴当且仅当
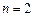 时,
时,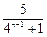 是整数, ∴
是整数, ∴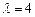
综上所
 述,当且仅当
述,当且仅当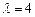 时,存在正整数
时,存在正整数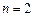 ,使等式
,使等式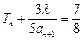 成立.
成立.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
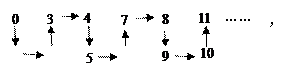
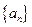 的前
的前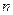 项和
项和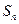 满足
满足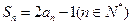 ,那么数列
,那么数列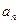 = .
= .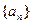 中,
中,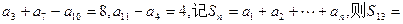
 78
78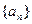 中,
中,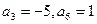 ,此数列的通项公式为 ,设
,此数列的通项公式为 ,设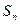 是数列
是数列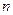 项和,则
项和,则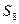 等于 。
等于 。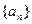 满足:
满足: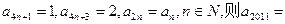 ,
,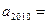 。
。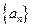 满足
满足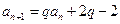 (
(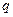 为常数,
为常数,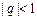 ),若
),若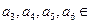
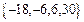 ,则
,则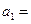 ▲ .
▲ .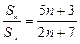 ,则
,则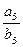 的值是( )
的值是( )