题目内容
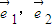 是两个不共线的向量,已知
是两个不共线的向量,已知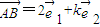 ,
,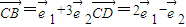 ,且A,B,D三点共线,则实数k= .
,且A,B,D三点共线,则实数k= .
【答案】分析:先由A,B,D三点共线,可构造两个向量共线,然后再利用两个向量共线的定理建立等式,解之即可.
解答:解:∵A,B,D三点共线,∴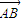 与
与  共线,
共线,
∴存在实数λ,使得 =
= ;
;
∵ =2
=2 -
-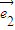 -(
-( +3
+3 )=
)= -4
-4 ,
,
∴2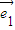 +k
+k =λ(
=λ(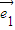 -4
-4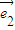 ),
),
∵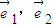 是平面内不共线的两向量,
是平面内不共线的两向量,
∴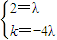 解得k=-8.
解得k=-8.
故答案为:-8
点评:本题主要考查了三点共线,以及平面向量数量积的性质及其运算律,属于基础题.
解答:解:∵A,B,D三点共线,∴
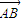 与
与  共线,
共线,∴存在实数λ,使得
 =
= ;
;∵
 =2
=2 -
-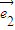 -(
-( +3
+3 )=
)= -4
-4 ,
,∴2
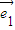 +k
+k =λ(
=λ(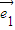 -4
-4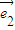 ),
),∵
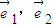 是平面内不共线的两向量,
是平面内不共线的两向量,∴
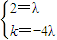 解得k=-8.
解得k=-8.故答案为:-8
点评:本题主要考查了三点共线,以及平面向量数量积的性质及其运算律,属于基础题.

练习册系列答案
相关题目