题目内容
【题目】如图,在四棱锥S﹣ABCD中,侧面SCD为钝角三角形且垂直于底面ABCD,![]() ,点M是SA的中点,
,点M是SA的中点,![]() ,
,![]() ,
,![]() .
.
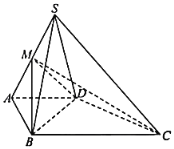
(1)求证:![]() 平面SCD;
平面SCD;
(2)若直线SD与底面ABCD所成的角为![]() ,求平面MBD与平面SBC所成的锐二面角的余弦值.
,求平面MBD与平面SBC所成的锐二面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)取![]() 中点
中点![]() ,连接
,连接![]() ,设
,设![]() ,
,![]() ,由已知可得
,由已知可得![]() ,则
,则![]() ,又平面
,又平面![]() 底面
底面![]() ,由面面垂直的性质可得
,由面面垂直的性质可得![]() 平面
平面![]() ;
;
(2)过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() ,可得
,可得![]() ,则
,则![]() 底面
底面![]() ,故
,故![]() 为斜线
为斜线![]() 在底面
在底面![]() 内的射影,求解三角形可得
内的射影,求解三角形可得![]() ,从而
,从而![]() ,过点
,过点![]() 作
作![]() ,则
,则![]() 底面
底面![]() ,可得
,可得![]() 、
、![]() 、
、![]() 两两垂直,以点
两两垂直,以点![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴正方向,
轴正方向,![]() 为
为![]() 轴正方向,
轴正方向,![]() 为
为![]() 轴正方向建立空间直角坐标系,然后分别求出平面
轴正方向建立空间直角坐标系,然后分别求出平面![]() 与平面
与平面![]() 的一个法向量,由两法向量所成角的余弦值可得平面
的一个法向量,由两法向量所成角的余弦值可得平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
解:(1)证明:取BC的中点E,连接DE,
设![]() ,
,![]() ,
,
依题意,四边形ABED为正方形,
且有![]()
![]() ,
,
![]() ,则
,则![]() .
.
又平面![]() 底面ABCD,平面
底面ABCD,平面![]() 底面
底面![]() ,
,
![]() 平面SCD;
平面SCD;
(2)解:过点S作CD的垂线,交CD延长线于点H,连接AH,
![]() 平面
平面![]() 底面ABCD,
底面ABCD,
平面![]() 底面
底面![]()
![]() ,
,
![]() 平面SCD,
平面SCD,![]() 底面ABCD,
底面ABCD,
故DH为斜线SD在底面ABCD内的射影,
![]() 为斜线SD与底面ABCD所成的角,即
为斜线SD与底面ABCD所成的角,即![]() .
.
由(1)得,![]() ,
,![]() 在
在![]() 中,
中,![]() ,
,![]() ,
,
在![]() 中,
中,![]()
![]()
![]() ,
,
由余弦定理得![]() ,
,
![]() ,从而
,从而![]() ,
,
过点D作![]() ,
,![]() 底面ABCD,
底面ABCD,
![]() DB、DC、DF两两垂直,
DB、DC、DF两两垂直,
如图,以点D为坐标原点,![]() 为x轴正方向,
为x轴正方向,![]() 为y轴正方向,
为y轴正方向,![]() 为z轴正方向建立空间直角坐标系,
为z轴正方向建立空间直角坐标系,
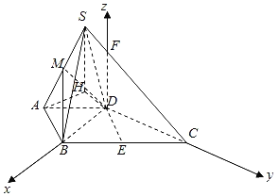
则![]()
![]()
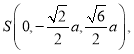
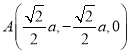 ,
,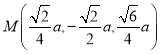 ,
,
设平面MBD的法向量![]() ,
,
由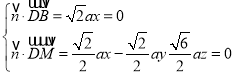 ,
,
取![]() ,得
,得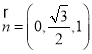 ;
;
设平面SBC的一个法向量为![]() ,
,
由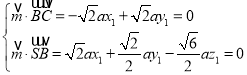 ,
,
取![]() ,得
,得![]() .
.
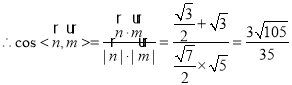 .
.
![]() 平面MBD与平面SBC所成的锐二面角的余弦值为
平面MBD与平面SBC所成的锐二面角的余弦值为![]() .
.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案【题目】下表是某电器销售公司2018年度各类电器营业收入占比和净利润占比统计表:
空调类 | 冰箱类 | 小家电类 | 其它类 | |
营业收入占比 | 90.10% | 4.98% | 3.82% | 1.10% |
净利润占比 | 95.80% |
| 3.82% | 0.86% |
则下列判断中不正确的是( )
A.该公司2018年度冰箱类电器销售亏损
B.该公司2018年度小家电类电器营业收入和净利润相同
C.该公司2018年度净利润主要由空调类电器销售提供
D.剔除冰箱类销售数据后,该公司2018年度空调类电器销售净利润占比将会降低
【题目】如表是我国某城市在2017年1月份至10月份个月最低温与最高温(![]() )的数据一览表.
)的数据一览表.
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
最高温 | 5 | 9 | 9 | 11 | 17 | 24 | 27 | 30 | 31 | 21 |
最低温 |
|
|
|
|
|
|
|
|
|
|
已知该城市的各月最低温与最高温具有相关关系,根据这一览表,则下列结论错误的是( )
A.最低温与最高位为正相关
B.每月最高温和最低温的平均值在前8个月逐月增加
C.月温差(最高温减最低温)的最大值出现在1月
D.1月至4月的月温差(最高温减最低温)相对于7月至10月,波动性更大
【题目】中国历法推测遵循以测为辅、以算为主的原则.例如《周髀算经》和《易经》里对二十四节气的晷(guǐ)影长的记录中,冬至和夏至的晷影长是实测得到的,其它节气的晷影长则是按照等差数列的规律计算得出的.下表为《周髀算经》对二十四节气晷影长的记录,其中![]() 寸表示115寸
寸表示115寸![]() 分(1寸=10分).
分(1寸=10分).
节气 | 冬至 | 小寒 (大雪) | 大寒 (小雪) | 立春 (立冬) | 雨水 (霜降) | 惊蛰 (寒露) | 春分 (秋分) | 清明 (白露) | 谷雨 (处暑) | 立夏 (立秋) | 小满 (大暑) | 芒种 (小暑) | 夏至 |
晷影长 (寸 | 135 |
|
|
|
|
| 75.5 |
|
|
|
|
| 16.0 |
已知《易经》中记录某年的冬至晷影长为130.0寸,夏至晷影长为14.8寸,按照上述规律那么《易经》中所记录的春分的晷影长应为( )
A.91.6寸B.82.0寸C.81.4寸D.72.4寸
【题目】中国历法推测遵循以测为辅、以算为主的原则.例如《周髀算经》和《易经》里对二十四节气的晷(guǐ)影长的记录中,冬至和夏至的晷影长是实测得到的,其它节气的晷影长则是按照等差数列的规律计算得出的.下表为《周髀算经》对二十四节气晷影长的记录,其中![]() 寸表示115寸
寸表示115寸![]() 分(1寸=10分).
分(1寸=10分).
节气 | 冬至 | 小寒 (大雪) | 大寒 (小雪) | 立春 (立冬) | 雨水 (霜降) | 惊蛰 (寒露) | 春分 (秋分) | 清明 (白露) | 谷雨 (处暑) | 立夏 (立秋) | 小满 (大暑) | 芒种 (小暑) | 夏至 |
晷影长 (寸 | 135 |
|
|
|
|
| 75.5 |
|
|
|
|
| 16.0 |
已知《易经》中记录某年的冬至晷影长为130.0寸,夏至晷影长为14.8寸,按照上述规律那么《易经》中所记录的春分的晷影长应为( )
A.91.6寸B.82.0寸C.81.4寸D.72.4寸
【题目】金秋九月,丹桂飘香,某高校迎来了一大批优秀的学生.新生接待其实也是和社会沟通的一个平台.校团委、学生会从在校学生中随机抽取了160名学生,对是否愿意投入到新生接待工作进行了问卷调查,统计数据如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女士 | 40 | 40 |
(1)根据上表说明,能否有99%把握认为愿意参加新生接待工作与性别有关;
(2)现从参与问卷调查且愿意参加新生接待工作的学生中,采用按性别分层抽样的方法,选取10人.若从这10人中随机选取3人到火车站迎接新生,设选取的3人中女生人数为![]() ,写出
,写出![]() 的分布列,并求
的分布列,并求![]() .
.
附: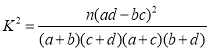 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |