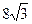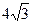题目内容
已知直线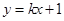 与椭圆
与椭圆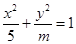 恒有公共点,则实数
恒有公共点,则实数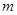 的取值范围为 ( )
的取值范围为 ( )
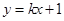 与椭圆
与椭圆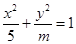 恒有公共点,则实数
恒有公共点,则实数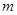 的取值范围为 ( )
的取值范围为 ( )A.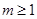 | B. | C.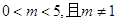 | D. |
D
由于直线y=kx+1恒过点M(0,1),直线y=kx+1与椭圆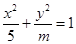 恒有公共点,则只要M(0,1)在椭圆的内部或在椭圆上
恒有公共点,则只要M(0,1)在椭圆的内部或在椭圆上
解答:解:由于直线y=kx+1恒过点M(0,1)
要使直线y=kx+1与椭圆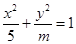 恒有公共点,则只要M(0,1)在椭圆的内部或在椭圆上
恒有公共点,则只要M(0,1)在椭圆的内部或在椭圆上
从而有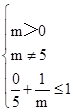 ,解可得m≥1且m≠5
,解可得m≥1且m≠5
故选D.
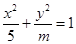 恒有公共点,则只要M(0,1)在椭圆的内部或在椭圆上
恒有公共点,则只要M(0,1)在椭圆的内部或在椭圆上解答:解:由于直线y=kx+1恒过点M(0,1)
要使直线y=kx+1与椭圆
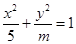 恒有公共点,则只要M(0,1)在椭圆的内部或在椭圆上
恒有公共点,则只要M(0,1)在椭圆的内部或在椭圆上从而有
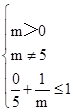 ,解可得m≥1且m≠5
,解可得m≥1且m≠5故选D.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
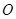 为坐标原点,
为坐标原点,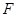 为椭圆
为椭圆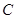 :
: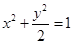 在
在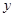 轴正半轴上的焦点,过
轴正半轴上的焦点,过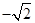 的直线
的直线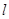 与
与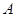 、
、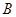 两点,点
两点,点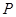 满足
满足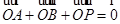 .
.
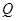 ,证明:
,证明: 的离心率是
的离心率是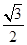 则双曲线
则双曲线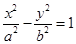 的离心率是()
的离心率是()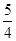
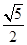
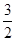
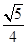
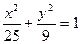 的两焦点为F1,F2,一直线过F1交椭圆于P、Q,则△PQF2的周长为 ___________.
的两焦点为F1,F2,一直线过F1交椭圆于P、Q,则△PQF2的周长为 ___________. 的共同焦点为F1,F2,P是两曲线的一个交点,则|PF1|·|PF2|的值为( )
的共同焦点为F1,F2,P是两曲线的一个交点,则|PF1|·|PF2|的值为( )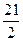
 圆心为A;动圆M过点
圆心为A;动圆M过点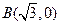 且与圆A相切,圆心M 的坐标为
且与圆A相切,圆心M 的坐标为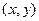 且
且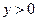 ,它的轨迹记为
,它的轨迹记为 C。
C。 C的方程;
C的方程;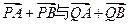 互相垂直?若存在,求出点P,Q的横坐标,若不存在,请说明理由。
互相垂直?若存在,求出点P,Q的横坐标,若不存在,请说明理由。

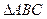 的顶点
的顶点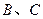 在椭圆
在椭圆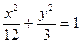 上,顶点
上,顶点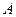 是椭圆的一个焦点,且椭圆的另外一个焦点在
是椭圆的一个焦点,且椭圆的另外一个焦点在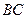 边上,则
边上,则