题目内容
 如图所示,已知AB⊥平面BCD,M、N分别是AC、AD的中点,BC⊥CD.
如图所示,已知AB⊥平面BCD,M、N分别是AC、AD的中点,BC⊥CD.(I)求证:MN∥平面BCD;
(II)求证:平面BCD⊥平面ABC;
(III)若AB=1,BC=
| 3 |
分析:(I)利用线面平行的判定定理:只需证明MN∥CD;
(II)利用面面垂直的判定定理转化为线面垂直,只需说明AB⊥平面BCD即可;
(III)因为AB⊥平面BCD,由线面角的定义可知∠ACB为直线AC与平面BCD所成的角,通过解直角三角形即可解得;
(II)利用面面垂直的判定定理转化为线面垂直,只需说明AB⊥平面BCD即可;
(III)因为AB⊥平面BCD,由线面角的定义可知∠ACB为直线AC与平面BCD所成的角,通过解直角三角形即可解得;
解答:解:(Ⅰ)因为M,N分别是AC,AD的中点,所以MN∥CD.
又MN?平面BCD且CD?平面BCD,
所以MN∥平面BCD.
(Ⅱ)因为AB⊥平面BCD,AB?平面ABC,
所以平面BCD⊥平面ABC.
(Ⅲ)因为AB⊥平面BCD,
所以∠ACB为直线AC与平面BCD所成的角.
在直角△ABC中,AB=1,BC=
,
所以tan∠ACB=
=
.所以∠ACB=30°.
故直线AC与平面BCD所成的角为30°.
又MN?平面BCD且CD?平面BCD,
所以MN∥平面BCD.
(Ⅱ)因为AB⊥平面BCD,AB?平面ABC,
所以平面BCD⊥平面ABC.
(Ⅲ)因为AB⊥平面BCD,
所以∠ACB为直线AC与平面BCD所成的角.
在直角△ABC中,AB=1,BC=
| 3 |
所以tan∠ACB=
| AB |
| BC |
| ||
| 3 |
故直线AC与平面BCD所成的角为30°.
点评:本题考查线面平行、面面垂直的判定,考查线面角的求解,属中档题,熟记相关判定定理及有关概念是解决问题的基础.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目

 如图所示,已知AB⊥平面BCD,M、N分别是AC、AD的中点,BC⊥CD.
如图所示,已知AB⊥平面BCD,M、N分别是AC、AD的中点,BC⊥CD. A:如图所示,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于点D,BC=4cm,
A:如图所示,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于点D,BC=4cm, 一次机器人足球比赛中,甲队1号机器人由点A开始作匀速直线运动,到达点B时,发现足球在点D处正以2倍于自己的速度向点A作匀速直线滚动.如图所示,已知
一次机器人足球比赛中,甲队1号机器人由点A开始作匀速直线运动,到达点B时,发现足球在点D处正以2倍于自己的速度向点A作匀速直线滚动.如图所示,已知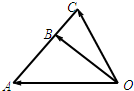 如图所示,已知
如图所示,已知