题目内容
【题目】“十三五”规划确定了到2020年消除贫困的宏伟目标，打响了精准扶贫的攻坚战，为完成脱贫任务，某单位在甲地成立了一家医疗器械公司吸纳附近贫困村民就工，已知该公司生产某种型号医疗器械的月固定成本为20万元，每生产1千件需另投入5.4万元，设该公司一月内生产该型号医疗器械x千件且能全部销售完，每千件的销售收入为
万元，已知
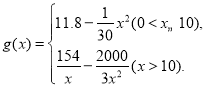
（1）请写出月利润y（万元）关于月产量x（千件）的函数解析式；
（2）月产量为多少千件时，该公司在这一型号医疗器械的生产中所获月利润最大？并求出最大月利润（精确到0.1万元）．
【答案】（1）
（2）当月产量为8千件时，该公司在这一型号医疗器械的生产中所获月利润最大，最大月利润为14.1万元．
【解析】
（1）分别求出
和
两种情况所对应的利润即可；
（2）利用导数及基本不等式求出（1）中分段函数的最大值即可.
解：（1）当时，
，
当时，
，
（2）①当
时，
，
令
，可得
时，
时，
，
时，
（万元）；
②当时，
（万元）（当且仅当
时取等号）．
综合①②知，当
时，y取最大值14.1，故当月产量为8千件时，该公司在这一型号医疗器械的生产中所获月利润最大，最大月利润为14.1万元．
【点晴】
本题主要考查函数模型的应用，考查学生数学建模能力，数学运算能力，是一道中档题.
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
