题目内容
记min{a,b}=
,设f(x)=min{sinx,cosx},x∈R,则f(x)的最大值是
.
|
| ||
| 2 |
| ||
| 2 |
分析:由正弦函数y=sinx与余弦函数y=cosx的图象即可得到答案.
解答:解:∵f(x)=min{sinx,cosx},x∈R,

由图可知,当x=2kπ+
(k∈Z)时,f(x)的最大值是
.
故答案为:
.

由图可知,当x=2kπ+
| π |
| 4 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查三角函数的最值,着重考查正弦函数y=sinx与余弦函数y=cosx的图象与性质,属于中档题.

练习册系列答案
相关题目
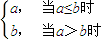 ,已知函数f(x)=min{x2+2tx+t2-1,x2-4x+3}是偶函数(t为实常数),则函数y=f(x)的零点为 .(写出所有零点)
,已知函数f(x)=min{x2+2tx+t2-1,x2-4x+3}是偶函数(t为实常数),则函数y=f(x)的零点为 .(写出所有零点)