题目内容
设a,b∈R,记min{a,b}=
,若函数f(x)=min{|x|,|x-2|}的图象关于直线x=m对称,则m的值为( )
|
| A、-2 | B、2 | C、-1 | D、1 |
分析:根据定义,作出函数f(x)的图象,利用数形结合确定函数的对称性即可求出m.
解答:解:∵记min{a,b}=
,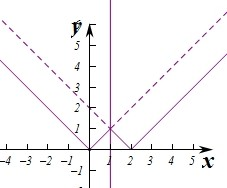
∴函数f(x)=min{|x|,|x-2|}对应的图象如图,
则由图象可知函数f(x)关于x=1对称,∴m=1.
故选:D.
|

∴函数f(x)=min{|x|,|x-2|}对应的图象如图,
则由图象可知函数f(x)关于x=1对称,∴m=1.
故选:D.
点评:本题主要考查函数新定义的应用,利用数形结合是解决本题的关键,比较基础.

练习册系列答案
相关题目