题目内容
已知数列{an}的前n项和Sn满足an+2SnSn-1="0" (n≥2),a1= ,求an.
,求an.
 ,求an.
,求an.an=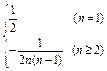 .
.
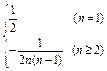 .
.∵当n≥2时,an=Sn-Sn-1,
∴Sn-Sn-1+2SnSn-1=0,
即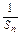 -
- =2, 4分
=2, 4分
∴数列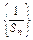 是公差为2的等差数列. 6分
是公差为2的等差数列. 6分
又S1=a1= ,∴
,∴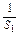 =2,
=2,
∴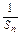 =2+(n-1)·2=2n,
=2+(n-1)·2=2n,
∴Sn= . 10分
. 10分
∴当n≥2时,an=-2SnSn-1=-2· ·
·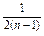
=-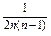 , 12分
, 12分
∴an=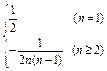 . 14分
. 14分
∴Sn-Sn-1+2SnSn-1=0,
即
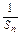 -
- =2, 4分
=2, 4分∴数列
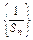 是公差为2的等差数列. 6分
是公差为2的等差数列. 6分又S1=a1=
 ,∴
,∴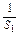 =2,
=2,∴
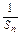 =2+(n-1)·2=2n,
=2+(n-1)·2=2n,∴Sn=
 . 10分
. 10分∴当n≥2时,an=-2SnSn-1=-2·
 ·
·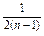
=-
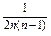 , 12分
, 12分∴an=
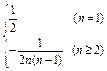 . 14分
. 14分
练习册系列答案
相关题目
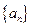 满足
满足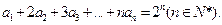
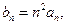 求数列
求数列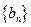 的前
的前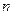 项和
项和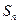 .
.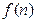 为正整数n(十进制)的各数位上的数字的平方之和,比如
为正整数n(十进制)的各数位上的数字的平方之和,比如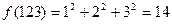 。记
。记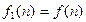 ,
,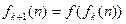 ,
,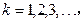 则
则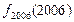 =
= 满足:
满足: ,则
,则 _______.
_______.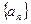 是递增数列,且对任意
是递增数列,且对任意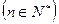 都有
都有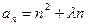 恒成立,则实数
恒成立,则实数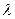 的取值范
的取值范

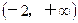

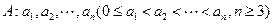 具有性质P:对任意
具有性质P:对任意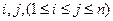 ,
,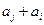 与
与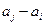 两数中至少有一个是该数列中的一项,现给出以下四
两数中至少有一个是该数列中的一项,现给出以下四 个命题:
个命题: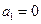 ;
;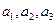
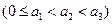 具有性质P,则
具有性质P,则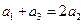 ;
;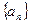 中,
中,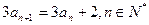 ,且
,且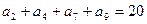 ,则
,则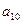 =" "
=" "  的第
的第 项
项 是二次函数,
是二次函数, ,求
,求 .
.