题目内容
(本小题满分12分)
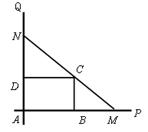
如下图,互相垂直的两条公路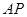 、
、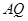 旁有一矩形花园
旁有一矩形花园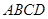 ,现欲将其扩建成一个更大的三角形花园
,现欲将其扩建成一个更大的三角形花园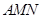 ,要求点
,要求点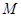 在射线
在射线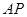 上,点
上,点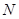 在射线
在射线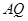 上,且直线
上,且直线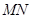 过点
过点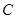 ,其中
,其中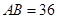 米,
米,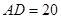 米. 记三角形花园
米. 记三角形花园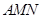 的面积为
的面积为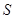 .
.
(Ⅰ)问: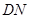 取何值时,
取何值时,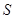 取得最小值,并求出最小值;
取得最小值,并求出最小值;
(Ⅱ)若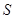 不超过1764平方米,求
不超过1764平方米,求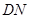 长的取值范围.
长的取值范围.
如下图,互相垂直的两条公路
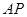 、
、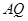 旁有一矩形花园
旁有一矩形花园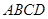 ,现欲将其扩建成一个更大的三角形花园
,现欲将其扩建成一个更大的三角形花园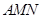 ,要求点
,要求点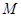 在射线
在射线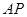 上,点
上,点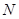 在射线
在射线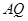 上,且直线
上,且直线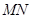 过点
过点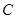 ,其中
,其中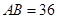 米,
米,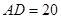 米. 记三角形花园
米. 记三角形花园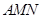 的面积为
的面积为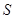 .
.
(Ⅰ)问:
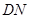 取何值时,
取何值时,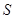 取得最小值,并求出最小值;
取得最小值,并求出最小值;(Ⅱ)若
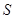 不超过1764平方米,求
不超过1764平方米,求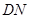 长的取值范围.
长的取值范围.(1)S的最小值等于1440平方米. ;(2)[8,50].
第一问利用设DN=X米(X>0),则AN=X+20.
因为DN/CN=AN/AM,所以X/36=(X+20)/AM,即AM=36(X+20)/X.
利用均值不等式得到结论。
第二问中由
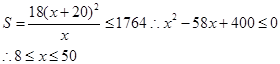 ………………10分
………………10分
解:(1)设DN=X米(X>0),则AN=X+20.
因为DN/CN=AN/AM,所以X/36=(X+20)/AM,即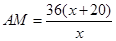 .
.
所以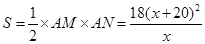 ……………………………4分
……………………………4分
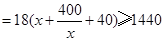 ,当且仅当X=20时取等号.
,当且仅当X=20时取等号.
所以,S的最小值等于1440平方米. ……………………………8分
(2)由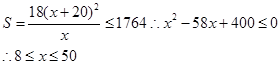
所以,DN长的取值范围是[8,50]. ………12分
因为DN/CN=AN/AM,所以X/36=(X+20)/AM,即AM=36(X+20)/X.
利用均值不等式得到结论。
第二问中由
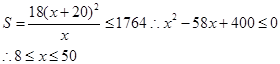 ………………10分
………………10分解:(1)设DN=X米(X>0),则AN=X+20.
因为DN/CN=AN/AM,所以X/36=(X+20)/AM,即
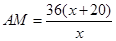 .
.所以
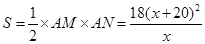 ……………………………4分
……………………………4分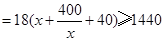 ,当且仅当X=20时取等号.
,当且仅当X=20时取等号.所以,S的最小值等于1440平方米. ……………………………8分
(2)由
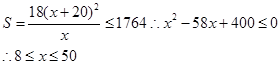
所以,DN长的取值范围是[8,50]. ………12分

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 是周期为
是周期为 的偶函数.当
的偶函数.当 时,
时, ,那么
,那么 _________.
_________.
 在区间
在区间 内函数的导数为正,且
内函数的导数为正,且 ≤0,则函数
≤0,则函数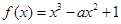 在区间
在区间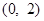 内单调递减,则实数
内单调递减,则实数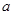 的取值范围是
的取值范围是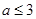
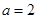
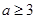
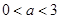
 则
则
 满足:对任意
满足:对任意 则下述式子中正确的是( )。
则下述式子中正确的是( )。


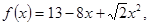 且
且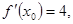 则
则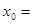
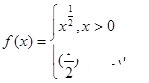 则
则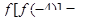




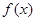 对于区间D内任意的
对于区间D内任意的 ,有
,有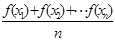
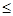
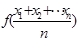 成立,称
成立,称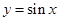 在区间
在区间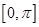 上是“凸函数”,则在△
上是“凸函数”,则在△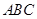 中,
中,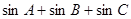 的最大值是( )
的最大值是( )


