题目内容
7.已知a>0,b>0,直线3x-4y=0是双曲线S:$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1的一条渐近线,双曲线S的离心率为e,则$\frac{3e+{a}^{2}}{b}$的最小值为( )| A. | $\frac{3\sqrt{5}}{2}$ | B. | $\frac{7\sqrt{5}}{2}$ | C. | $\frac{11\sqrt{5}}{3}$ | D. | $\frac{4\sqrt{15}}{3}$ |
分析 由题意,$\frac{a}{b}$=$\frac{3}{4}$,e=$\sqrt{1+(\frac{b}{a})^{2}}$=$\frac{5}{3}$,代入可得$\frac{3e+{a}^{2}}{b}$=$\frac{5+{a}^{2}}{\frac{4}{3}a}$=$\frac{3}{4}×(\frac{5}{a}+a)$,利用基本不等式,即可得出结论.
解答 解:由题意,$\frac{a}{b}$=$\frac{3}{4}$,e=$\sqrt{1+(\frac{b}{a})^{2}}$=$\frac{5}{3}$,
所以$\frac{3e+{a}^{2}}{b}$=$\frac{5+{a}^{2}}{\frac{4}{3}a}$=$\frac{3}{4}×(\frac{5}{a}+a)$≥$\frac{3}{4}×2\sqrt{5}$=$\frac{3\sqrt{5}}{2}$,
所以$\frac{3e+{a}^{2}}{b}$的最小值为$\frac{3\sqrt{5}}{2}$,
故选:A.
点评 本题考查双曲线的性质,考查基本不等式的运用,比较基础.

练习册系列答案
相关题目
17.设集合A={x|2x-1≥5},集合$B=\left\{{x|y=\frac{cosx}{{\sqrt{7-x}}}}\right\}$,则A∩B等于( )
| A. | (3,7) | B. | [3,7] | C. | (3,7] | D. | [3,7) |
2.已知函数f(x)=sinωx-$\sqrt{3}$cosωx(ω>0)的图象与x轴的两个相邻交点的距离等于$\frac{π}{2}$,若将函数y=f(x)的图象向左平移$\frac{π}{6}$个单位得到函数y=g(x)的图象,则y=g(x)是减函数的区间为( )
| A. | (-$\frac{π}{3}$,0) | B. | (-$\frac{π}{4}$,$\frac{π}{4}$) | C. | (0,$\frac{π}{3}$) | D. | ($\frac{π}{4}$,$\frac{π}{3}$) |
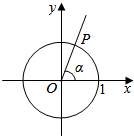 直角坐标系xOy中,锐角α的终边与单位圆的交点为P,将OP绕O逆时针旋转到OQ,使∠POQ=α,其中Q是OQ与单位圆的交点,设Q的坐标为(x,y).
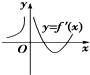
直角坐标系xOy中,锐角α的终边与单位圆的交点为P,将OP绕O逆时针旋转到OQ,使∠POQ=α,其中Q是OQ与单位圆的交点,设Q的坐标为(x,y). 设函数f(x)在定义域内可导且其图象如图①所示,则导函数y=f′(x)的图象最有可能是( )
设函数f(x)在定义域内可导且其图象如图①所示,则导函数y=f′(x)的图象最有可能是( )