题目内容
【题目】在圆![]() 内有一点
内有一点![]() ,
,![]() 为圆
为圆![]() 上一动点,线段
上一动点,线段![]() 的垂直平分线与
的垂直平分线与![]() 的连线交于点
的连线交于点![]() .
.
(Ⅰ)求点![]() 的轨迹方程.
的轨迹方程.
(Ⅱ)若动直线![]() 与点
与点![]() 的轨迹交于
的轨迹交于![]() 、
、![]() 两点,且以
两点,且以![]() 为直径的圆恒过坐标原点
为直径的圆恒过坐标原点![]() .问是否存在一个定圆与动直线
.问是否存在一个定圆与动直线![]() 总相切.若存在,求出该定圆的方程;若不存在,请说明理由.
总相切.若存在,求出该定圆的方程;若不存在,请说明理由.
【答案】(Ⅰ)![]() (Ⅱ)存在定圆
(Ⅱ)存在定圆![]() 总与直线
总与直线![]() 相切
相切
【解析】
(Ⅰ)由点![]() 在线段
在线段![]() 的上,结合垂直平分线的性质可得
的上,结合垂直平分线的性质可得![]() ,从而由椭圆的定义可得结果;(Ⅱ)直线
,从而由椭圆的定义可得结果;(Ⅱ)直线![]() 斜率不存在时,原点
斜率不存在时,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,直线
,直线![]() 斜率存在时,可设直线
斜率存在时,可设直线![]() 的方程为
的方程为![]() ,解
,解 消去
消去![]() 得方程:
得方程:![]() ,利用向量垂直数量积为零,结合韦达定理可得
,利用向量垂直数量积为零,结合韦达定理可得![]() ,由点点直线距离公式可得原点
,由点点直线距离公式可得原点![]() 到直线
到直线![]() 的距离
的距离![]() ,进而可得结果.
,进而可得结果.
(Ⅰ)圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]()
![]() 点
点![]() 在线段
在线段![]() 的垂直平分线上
的垂直平分线上 ![]()
![]()
又![]() 点
点![]() 在线段
在线段![]() 的上
的上 ![]()
![]()
![]() 由椭圆的定义可知点
由椭圆的定义可知点![]() 的轨迹是以
的轨迹是以![]() ,
,![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆,
的椭圆,
![]()
![]() ,故点
,故点![]() 的轨迹方程为
的轨迹方程为![]()
(Ⅱ)假设存在这样的圆.设![]() ,
, ![]() .
.
由已知,以![]() 为直径的圆恒过原点
为直径的圆恒过原点![]() ,即
,即![]() ,所以
,所以![]() .
.
当直线![]() 垂直于
垂直于![]() 轴时,
轴时, ![]() ,
, ![]() ,所以
,所以![]() ,又
,又![]() ,解得
,解得![]() ,
,
不妨设![]() ,
,![]() 或
或![]() ,
,![]() ,即直线
,即直线![]() 的方程为
的方程为![]() 或
或![]() ,此时原点
,此时原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
当直线![]() 的斜率存在时,可设直线
的斜率存在时,可设直线![]() 的方程为
的方程为![]() ,解
,解 消去
消去![]() 得方程:
得方程: ![]() 因为直线
因为直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,所以方程的判别式
两点,所以方程的判别式
![]() 即
即![]() ,且
,且![]() ,
, ![]() .
.
由![]() ,得
,得![]()
![]() ,
,
所以![]() 整理得
整理得![]() (满足
(满足![]() ).
).
所以原点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
综上所述,原点![]() 到直线
到直线![]() 的距离为定值
的距离为定值![]() ,即存在定圆
,即存在定圆![]() 总与直线
总与直线![]() 相切.
相切.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格(千元) | 23 | 30 | 22 | 7 |
(1)写出价格![]() 关于时间
关于时间![]() 的函数关系式;(
的函数关系式;(![]() 表示投放市场的第
表示投放市场的第![]() 天);
天);
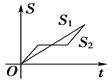
(2)销售量![]() 与时间
与时间![]() 的函数关系:
的函数关系:![]() ,则该产品投放市场第几天销售额最高?最高为多少千元?
,则该产品投放市场第几天销售额最高?最高为多少千元?