题目内容
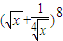展开式中含x的整数次幂的项的系数之和为 （用数字作答）．
【答案】分析：利用二项展开式的通项公式进行找寻整数次幂，注意找到所有的整数次幂，然后再求和．
解答：解：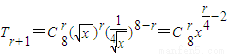
，
当r=0，4，8时为含x的整数次幂的项，
所以展开式中含x的整数次幂的项的系数之和为C8+C84+C88=72，
填72．
点评：本题考查二项展开式的通项公式，考查转化思想和化归思想，考查学生们的运算能力．
解答：解：
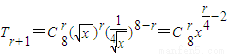，当r=0，4，8时为含x的整数次幂的项，
所以展开式中含x的整数次幂的项的系数之和为C8+C84+C88=72，
填72．
点评：本题考查二项展开式的通项公式，考查转化思想和化归思想，考查学生们的运算能力．
练习册系列答案
同步练习强化拓展系列答案
相关题目
若(3x+
)n的展开式中各项系数之和为256，则展开式中含x的整数次幂的项共有（ ）
| 1 | ||
|
| A、1项 | B、2项 | C、3项 | D、4项 |
若（3x+
）n的展开式中各项系数之和为1024，则展开式中含x的整数次幂的项共有（ ）
| 1 | ||
|
| A、3项 | B、4项 | C、5项 | D、6项 |
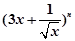的展开式中各项系数之和为256，则展开式中含x的整数次幂的项共有（ ）
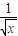）n的展开式中各项系数之和为1024，则展开式中含x的整数次幂的项共有（ ）