题目内容
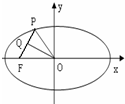 如图,P是椭圆
如图,P是椭圆| x2 |
| 25 |
| y2 |
| 9 |
| OQ |
| 1 |
| 2 |
| OP |
| OF |
| OQ |
A、
| ||
B、
| ||
C、
| ||
| D、10 |
分析:由
=
(
+
)可以推出Q是线段PF的中点,由P在椭圆上及 |
|=4,通过解方程组求得P点横坐标为 -
,再求出到左准线的距离.
| OQ |
| 1 |
| 2 |
| OP |
| OF |
| OQ |
| 15 |
| 4 |
解答:解:∵
=
(
+
),
∴Q是线段PF的中点,
∵由P在椭圆上且 |
|=4,设P(a,b),F(-4,0),Q(
,
),
∴
,∴a=-
,
椭圆左准线x=-
.
∴点P到该椭圆左准线的距离 d=(-
) -(-
)=
.
故选A.
| OQ |
| 1 |
| 2 |
| OP |
| OF |
∴Q是线段PF的中点,
∵由P在椭圆上且 |
| OQ |
| a-4 |
| 2 |
| b |
| 2 |
∴
|
| 15 |
| 4 |
椭圆左准线x=-
| 25 |
| 4 |
∴点P到该椭圆左准线的距离 d=(-
| 15 |
| 4 |
| 25 |
| 4 |
| 5 |
| 2 |
故选A.
点评:该题考查向量的线性表示以及椭圆的几何性质,另外还考查运算能力.是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
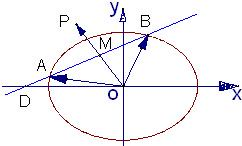 如图,已知过点D(-2,0)的直线l与椭圆
如图,已知过点D(-2,0)的直线l与椭圆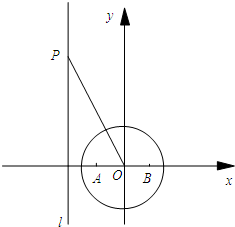 如图,圆O的方程为x2+y2=2,直线l是椭圆
如图,圆O的方程为x2+y2=2,直线l是椭圆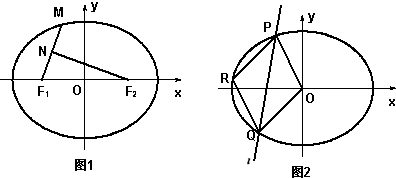
 (2011•嘉定区三模)如图,已知椭圆
(2011•嘉定区三模)如图,已知椭圆