题目内容
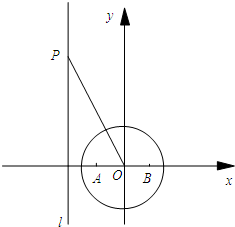 如图,圆O的方程为x2+y2=2,直线l是椭圆
如图,圆O的方程为x2+y2=2,直线l是椭圆| x2 | 2 |
(Ⅰ)若点P的纵坐标为4,求此时点Q的坐标,并说明此时直线PQ与圆O的位置关系;
(Ⅱ)求当∠APB取得最大值时P点的坐标.
分析:(Ⅰ)由题意得A(-1,0),B(1,0),直线l的方程为x=-2,直线AQ的方程为x-2y+1=0.由
,解得Q点的坐标为 (-
,-
)或(1,1).由此能推导出PQ与圆O相切.
(Ⅱ)设P点在x轴上方,设P(-2,m)(m>0).设准线l与x轴交于点Q,记 BPQ=α,APQ=β,所以tan∠APB=tan(α-β)=
≤
=
.由此能求出当∠APB取得最大值时P点的坐标.
|
| 7 |
| 5 |
| 1 |
| 5 |
(Ⅱ)设P点在x轴上方,设P(-2,m)(m>0).设准线l与x轴交于点Q,记 BPQ=α,APQ=β,所以tan∠APB=tan(α-β)=
| ||||
1+
|
| 2 | ||||
2
|
| ||
| 3 |
解答:解:(Ⅰ)由题意得A(-1,0),B(1,0),直线l的方程为x=-2,
∴P(-2,4),
∴kOP=
=-2,
∵AQ⊥OP,
∴kAQ=
.
∴直线AQ的方程为y=
(x+1),即x-2y+1=0.
由
,消去x并整理得5y2-4y-1=0.
解得y=1,或y=-
.
当y=1时x=1,当 y=-
时,xx=-
.
∴Q点的坐标为 (-
,-
)或(1,1).
当Q为(1,1)时,直线PQ的方程x+y-2=0.
圆心O到直线的距离为
=
,∴PQ与圆O相切.
同理可得,当Q为(-
,-
) 时,PQ也与圆O相切.
(Ⅱ)不妨设P点在x轴上方,设P(-2,m)(m>0).
设准线l与x轴交于点Q,记 BPQ=α,APQ=β,
∴tan∠APB=tan(α-β)
=
=
=
≤
=
.
当且仅当m=
时取得等号.
显然 APB为锐角,故 APB的最大值为30°,
此时P点的坐标(-2,±
).
∴P(-2,4),
∴kOP=
| 4 |
| 0-2 |
∵AQ⊥OP,
∴kAQ=
| 1 |
| 2 |
∴直线AQ的方程为y=
| 1 |
| 2 |
由
|
解得y=1,或y=-
| 1 |
| 5 |
当y=1时x=1,当 y=-
| 1 |
| 5 |
| 7 |
| 5 |
∴Q点的坐标为 (-
| 7 |
| 5 |
| 1 |
| 5 |
当Q为(1,1)时,直线PQ的方程x+y-2=0.
圆心O到直线的距离为
| 2 | ||
|
| 2 |
同理可得,当Q为(-
| 7 |
| 5 |
| 1 |
| 5 |
(Ⅱ)不妨设P点在x轴上方,设P(-2,m)(m>0).
设准线l与x轴交于点Q,记 BPQ=α,APQ=β,
∴tan∠APB=tan(α-β)
=
| tanα-tanβ |
| 1+tanαtanβ |
=
| ||||
1+
|
=
| 2 | ||
m+
|
≤
| 2 | ||||
2
|
=
| ||
| 3 |
当且仅当m=
| 3 |
显然 APB为锐角,故 APB的最大值为30°,
此时P点的坐标(-2,±
| 3 |
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,圆O的方程为x2+y2=4,
如图,圆O的方程为x2+y2=4,
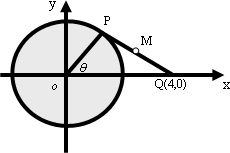
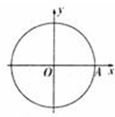 如图,圆O的方程为x2+y2=4,(1)已知点A的坐标为(2,0),B为圆周上任意一点,求弧
如图,圆O的方程为x2+y2=4,(1)已知点A的坐标为(2,0),B为圆周上任意一点,求弧 长小于π的概率;(2)若P(x,y)为圆O内任意一点,求P到原点的距离大于1的概率.
长小于π的概率;(2)若P(x,y)为圆O内任意一点,求P到原点的距离大于1的概率.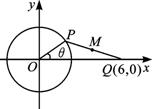
 长小于π的概率;
长小于π的概率;