题目内容
数列{an}的首项a1=1,前n项和Sn满足2kSn-(2k+1)Sn-1=2k(常数k>0,n=2,3,4…)(Ⅰ)求证:数列{an}是等比数列;
(Ⅱ)设数列{an}的公比为f(k),作数列{bn},使b1=3,bn=f(![]() )(n=2,3,4,…)求数列{bn}的通项公式;
)(n=2,3,4,…)求数列{bn}的通项公式;
(Ⅲ)设cn=bn-2,若存在m∈N*,且m<n;使![]() (cmcm+1+cm+lcm+2+…+cncn+1)<
(cmcm+1+cm+lcm+2+…+cncn+1)<![]() ,试求m的最小值.
,试求m的最小值.
解:(Ⅰ)证明:当n≥2时,2kSn-(2k+1)Sn-1=2k
∴2k(Sn-Sn-1)-Sn-1=2k,即2kan-Sn-1=2k ①
∴2kan+1-Sn=2k ②
②-①得2kn+1-2kan-an=0,即2kan+1=(2k+1)an
由①a2=1+![]() ,∴
,∴![]() =l+
=l+![]()
又![]() 符合上式.∴{an}是以1为首项,l+
符合上式.∴{an}是以1为首项,l+![]() 为公比的等比数列
为公比的等比数列
(Ⅱ)解:由(Ⅰ)及f(k)=1+![]() ,∴bn=f(
,∴bn=f(![]() )=1+
)=1+![]() bn-1(n≥2)
bn-1(n≥2)
∴bn-2=![]() (bn-1-2)又b1=3,即b2-2=1,∴
(bn-1-2)又b1=3,即b2-2=1,∴![]() ,
,
∴{bn-2}是以1为首项,为公比的等比数列
∴bn-2=(![]() )n-1,∴bn=2+(
)n-1,∴bn=2+(![]() )n-1
)n-1
(Ⅲ)由(Ⅱ)知cn=bn-2=(![]() )n-1,则cn·cn+1=(
)n-1,则cn·cn+1=(![]() )2n-1,
)2n-1,
∴![]() (cmcm+1+cm+1,cm+2+…+cncn+1)=
(cmcm+1+cm+1,cm+2+…+cncn+1)=![]()
![]()
=![]()
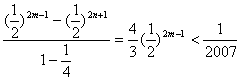 ∴
∴![]()
∵512<669<1 024,∴2m-3>9,即m>6
又m∈N*,∴m的最小值为7.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目