题目内容
(2014·大庆模拟)已知向量a=( ,cosωx),b=(sinωx,1),函数f(x)=a·b,且最小正周期为4π.
,cosωx),b=(sinωx,1),函数f(x)=a·b,且最小正周期为4π.
(1)求ω的值.
(2)设α,β∈ ,f
,f =
= ,f
,f =-
=- ,求sin(α+β)的值.
,求sin(α+β)的值.
(3)若x∈[-π,π],求函数f(x)的值域.
 ,cosωx),b=(sinωx,1),函数f(x)=a·b,且最小正周期为4π.
,cosωx),b=(sinωx,1),函数f(x)=a·b,且最小正周期为4π.(1)求ω的值.
(2)设α,β∈
 ,f
,f =
= ,f
,f =-
=- ,求sin(α+β)的值.
,求sin(α+β)的值.(3)若x∈[-π,π],求函数f(x)的值域.
(1) (2)
(2)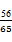 (3)
(3)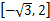
 (2)
(2)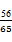 (3)
(3)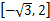
(1)由已知,易得f(x)= sinωx+cosωx
sinωx+cosωx
=2sin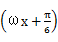 ,
,
f(x)的最小正周期为4π,即T=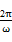 =4π,解得ω=
=4π,解得ω= .
.
(2)由(1)知,f(x)=2sin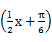 ,
,
则f =2sin
=2sin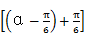 =2sinα=
=2sinα= ,
,
所以sinα= ,又α∈
,又α∈ ,
,
所以cosα=- .
.
同理f =2sin
=2sin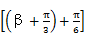
=2sin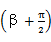 =2cosβ=-
=2cosβ=- ,
,
所以cosβ=-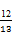 ,又β∈
,又β∈ ,
,
所以sinβ=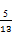 ,
,
所以sin(α+β)=sinαcosβ+cosαsinβ=-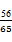 .
.
(3)当x∈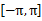 时,-
时,- ≤
≤ x+
x+ ≤
≤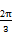 ,
,
令t= x+
x+ ,则t∈
,则t∈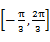 ,
,
原函数可化为f(t)=2sint,t∈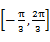 .
.
当t=- 时,f(t)min=-
时,f(t)min=- ;
;
当t= 时,f(t)max=2.
时,f(t)max=2.
所以,函数f(x)的值域为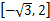 .
.
 sinωx+cosωx
sinωx+cosωx=2sin
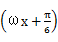 ,
,f(x)的最小正周期为4π,即T=
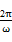 =4π,解得ω=
=4π,解得ω= .
.(2)由(1)知,f(x)=2sin
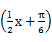 ,
,则f
 =2sin
=2sin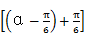 =2sinα=
=2sinα= ,
,所以sinα=
 ,又α∈
,又α∈ ,
,所以cosα=-
 .
.同理f
 =2sin
=2sin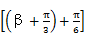
=2sin
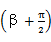 =2cosβ=-
=2cosβ=- ,
,所以cosβ=-
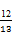 ,又β∈
,又β∈ ,
,所以sinβ=
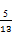 ,
,所以sin(α+β)=sinαcosβ+cosαsinβ=-
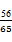 .
.(3)当x∈
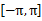 时,-
时,- ≤
≤ x+
x+ ≤
≤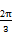 ,
,令t=
 x+
x+ ,则t∈
,则t∈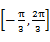 ,
,原函数可化为f(t)=2sint,t∈
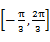 .
.当t=-
 时,f(t)min=-
时,f(t)min=- ;
;当t=
 时,f(t)max=2.
时,f(t)max=2.所以,函数f(x)的值域为
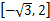 .
.
练习册系列答案
相关题目

 的图形向右平移
的图形向右平移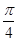 个单位后得到
个单位后得到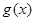 的图像,已知
的图像,已知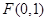 ,与x轴相交于点P、Q,点M为最高点,且
,与x轴相交于点P、Q,点M为最高点,且 的面积为
的面积为 .
.
 中,
中, 分别是角A,B,C的对边,
分别是角A,B,C的对边,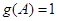 ,且
,且 ,求
,求 。(1)在一个周期内
。(1)在一个周期内 如图所示,试根据图象写出
如图所示,试根据图象写出 秒的时内I能同时取最大值|A|和最小值-|A|,那么正整数
秒的时内I能同时取最大值|A|和最小值-|A|,那么正整数 的最小值为多少?
的最小值为多少?
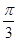 ,x=
,x=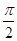 都是函数f(x)=sin(ωx+φ)(ω>0,-π<φ≤π)的对称轴,且函数f(x)在区间
都是函数f(x)=sin(ωx+φ)(ω>0,-π<φ≤π)的对称轴,且函数f(x)在区间 上单调递减,则( )
上单调递减,则( )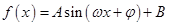 (A>0,ω>0)的一系列对应值如下表:
(A>0,ω>0)的一系列对应值如下表: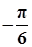
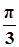
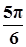
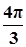

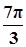
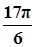
 (k>0)周期为
(k>0)周期为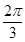 ,当x∈[0,
,当x∈[0, ]时,方程
]时,方程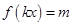 恰有两个不同的解,求实数m的取值范围;
恰有两个不同的解,求实数m的取值范围;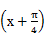 的图象沿x轴向右平移a个单位(a>0),所得图象关于y轴对称,则a的最小值为( )
的图象沿x轴向右平移a个单位(a>0),所得图象关于y轴对称,则a的最小值为( )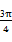


 ,
, 并求
并求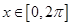 时,求f(x)的最小值以及取得最小值时x的集合.
时,求f(x)的最小值以及取得最小值时x的集合. ),y=f(x)的部分图象如图所示,则f(
),y=f(x)的部分图象如图所示,则f( )=______.
)=______.
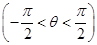 的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P
的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P ,则φ的值可以是( )
,则φ的值可以是( )


