题目内容
已知函数f(x)=x3-ax2-3x.
(1)若f(x)在区间[1,+∞)上是增函数,求实数a的取值范围;
(2)若x=-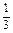 是f(x)的极值点,求f(x)在[1,a]上的最大值;
是f(x)的极值点,求f(x)在[1,a]上的最大值;
(3)在(2)的条件下,是否存在实数b,使得函数g(x)=bx的图象与函数f(x)的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
(1)若f(x)在区间[1,+∞)上是增函数,求实数a的取值范围;
(2)若x=-
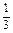 是f(x)的极值点,求f(x)在[1,a]上的最大值;
是f(x)的极值点,求f(x)在[1,a]上的最大值;(3)在(2)的条件下,是否存在实数b,使得函数g(x)=bx的图象与函数f(x)的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
(1)a≤0(2)f(x)在[1,4]上的最大值是f(1)=-6(3)存在符合条件的实数b,b的范围为b>-7且b≠- 3
(1)f′(x)=3x2-2ax-3
∵f(x)在[1,+∞)上是增函数,
∴f′(x)在[1,+∞)上恒有f′(x)≥0,
即3x2-2ax-3≥0在[1,+∞)上恒成立
则必有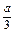 ≤1且f′(1)=-2a≥0,∴a≤0.
≤1且f′(1)=-2a≥0,∴a≤0.
(2)依题意,f′(-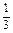 )=0,即
)=0,即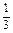 +
+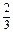 a-3=0
a-3=0
∴a=4,∴f(x)=x3-4x2-3x
令f′(x)=3x2-8x-3=0,
得x1=-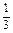 ,x2=3.则
,x2=3.则
当x变化时,f′(x),f(x)的变化情况如下表:
∴f(x)在[1,4]上的最大值是f(1)=-6.
(3)函数g(x)=bx的图象与函数f(x)的图象恰有3个交点,即方程x3-4x2-3x=bx恰有3个不等实根
∴x3-4x2-3x-bx=0,∴x=0是其中一个根,
∴方程x2-4x-3-b=0有两个非零不等实根,
∴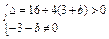 ,∴b>-7且b≠-3.
,∴b>-7且b≠-3.
∴存在符合条件的实数b,b的范围为b>-7且b≠- 3.
∵f(x)在[1,+∞)上是增函数,
∴f′(x)在[1,+∞)上恒有f′(x)≥0,
即3x2-2ax-3≥0在[1,+∞)上恒成立
则必有
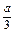 ≤1且f′(1)=-2a≥0,∴a≤0.
≤1且f′(1)=-2a≥0,∴a≤0.(2)依题意,f′(-
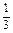 )=0,即
)=0,即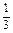 +
+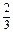 a-3=0
a-3=0∴a=4,∴f(x)=x3-4x2-3x
令f′(x)=3x2-8x-3=0,
得x1=-
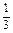 ,x2=3.则
,x2=3.则当x变化时,f′(x),f(x)的变化情况如下表:
| x | 1 | (1,3) | 3 | (3,4) | 4 |
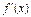 | | - | 0 | + | |
| f (x) | -6 |  | -18 | 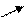 | -12 |
(3)函数g(x)=bx的图象与函数f(x)的图象恰有3个交点,即方程x3-4x2-3x=bx恰有3个不等实根
∴x3-4x2-3x-bx=0,∴x=0是其中一个根,
∴方程x2-4x-3-b=0有两个非零不等实根,
∴
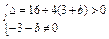 ,∴b>-7且b≠-3.
,∴b>-7且b≠-3.∴存在符合条件的实数b,b的范围为b>-7且b≠- 3.

练习册系列答案
相关题目
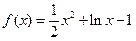 .
.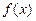 在区间
在区间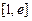 (
(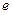 为自然对数的底)上的最大值和最小值;
为自然对数的底)上的最大值和最小值;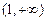 上,函数
上,函数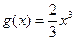 的图象的下方;
的图象的下方;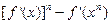 ≥
≥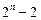
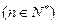 .
.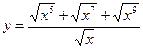
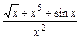 ;
;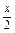 (1-2cos2
(1-2cos2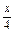 );
);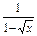 +
+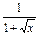 .
.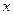 的三次函数
的三次函数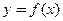 的两个极值点为P、Q,其中P为原点,Q在曲线
的两个极值点为P、Q,其中P为原点,Q在曲线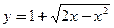 上,则曲线
上,则曲线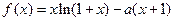 ,其中
,其中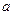 为常数.
为常数.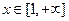 时,
时,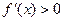 恒成立,求
恒成立,求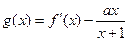 的单调区间.
的单调区间.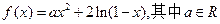 。
。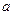 ,使得
,使得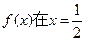 处取极值?试证明你的结论;
处取极值?试证明你的结论;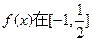 上是减函数,求实数
上是减函数,求实数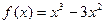 ,给出下列四个命题:①
,给出下列四个命题:①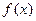 是增函数,无极值;②
是增函数,无极值;②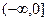 及
及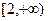 上是增函数;④
上是增函数;④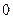 ,极小值
,极小值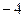 ;其中正确命题的个数为( )
;其中正确命题的个数为( )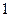
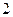

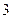
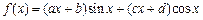 ,试确定常数
,试确定常数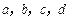 ,使得
,使得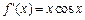 .
.