题目内容
(本小题满分16分)
椭圆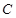 :
: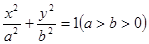 的左、右顶点分别
的左、右顶点分别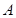 、
、 ,椭圆过点
,椭圆过点 且离心率
且离心率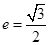 .
.
(1)求椭圆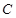 的标准方程;
的标准方程;
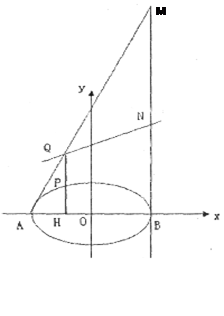
(2)过椭圆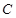 上异于
上异于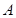 、
、 两点的任意一点
两点的任意一点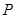 作
作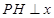 轴,
轴,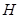 为垂足,延长
为垂足,延长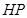 到点
到点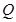 ,且
,且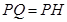 ,过点
,过点 作直线
作直线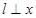 轴,连结
轴,连结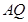 并延长交直线
并延长交直线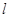 于点
于点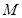 ,线段
,线段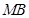 的中点记为点
的中点记为点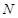 .
.
①求点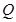 所在曲线的方程;
所在曲线的方程;
②试判断直线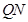 与以
与以 为直径的圆
为直径的圆 的位置关系, 并证明.
的位置关系, 并证明.
(1)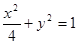 (2)①
(2)①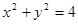 ②直线与圆相切,证明:AQ的方程为
②直线与圆相切,证明:AQ的方程为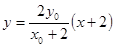 ,
,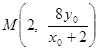 ,
,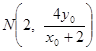 ,
,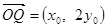 ,
,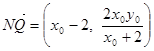 ,
,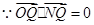 ∴
∴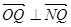 ,∴直线QN与圆O相切
,∴直线QN与圆O相切
解析试题分析:(1)因为椭圆经过点(0,1),所以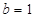 ,又椭圆的离心率
,又椭圆的离心率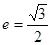 得
得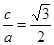 ,
,
即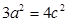 ,由
,由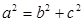 得
得 ,所以
,所以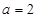 ,
,
故所求椭圆方程为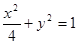 。
。
(2)①设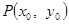 ,则
,则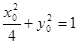 ,设
,设 ,∵HP=PQ,∴
,∵HP=PQ,∴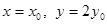 即
即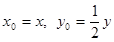 ,将
,将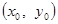 代入
代入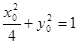 得
得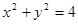 ,
,
所以Q点在以O为圆心,2为半径的圆上,即Q点在以AB为直径的圆O上。
②又A(-2,0),直线AQ的方程为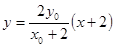 ,令
,令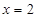 ,则
,则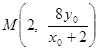 ,
,
又B(2,0),N为MB的中点,∴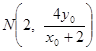 ,
,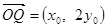 ,
,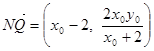
∴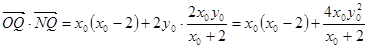
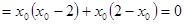 ,∴
,∴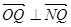 ,∴直线QN与圆O相切。
,∴直线QN与圆O相切。
考点:椭圆方程,动点的轨迹方程及直线与圆的位置关系
点评:最后一问判断直线与圆的位置关系转化为向量简化了解题

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
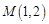 ,它们在
,它们在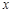 轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点.
轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点.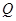 ,点
,点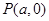 都满足
都满足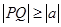 ,求
,求 的取值范围.
的取值范围.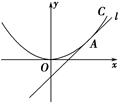
 ,长轴长为
,长轴长为 ,离心率
,离心率 ,过右焦点
,过右焦点 的直线
的直线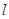 交
交 ,
, 两点:
两点: 的面积;
的面积;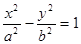 的离心率
的离心率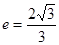 ,过
,过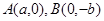 的直线到原点的距离是
的直线到原点的距离是
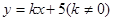 交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值. 轴的距离少1.
轴的距离少1.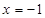 于
于 点,且
点,且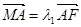 ,
,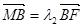 ,
,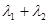 的值。
的值。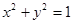 过椭圆
过椭圆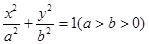 的两焦点,与椭圆有且仅有两个
的两焦点,与椭圆有且仅有两个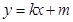 与圆
与圆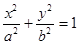 相交于
相交于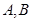 两点记
两点记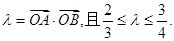
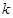 的取值范围;
的取值范围;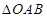 的面积S的取值范围.
的面积S的取值范围. 是椭圆
是椭圆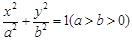 上一点,
上一点,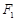 ,
,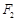 是椭圆的两焦点,且满足
是椭圆的两焦点,且满足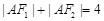
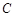 、
、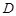 是椭圆上任两点,且直线
是椭圆上任两点,且直线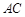 、
、 的斜率分别为
的斜率分别为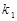 、
、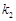 ,若存在常数
,若存在常数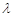 使
使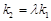 ,求直线
,求直线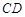 的斜率.
的斜率. 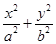 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+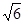 =0相切。
=0相切。