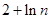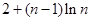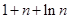题目内容
已知数列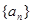 的前
的前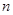 项和
项和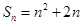 ,设数列
,设数列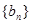 满足
满足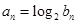 ,
,
(1)求数列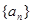 的通项公式;
的通项公式;
(2)求数列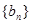 的前
的前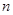 项和
项和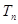 ;
;
(3)设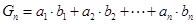 ,求
,求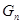 .
.
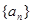 的前
的前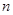 项和
项和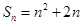 ,设数列
,设数列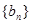 满足
满足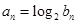 ,
,(1)求数列
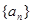 的通项公式;
的通项公式;(2)求数列
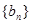 的前
的前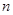 项和
项和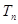 ;
;(3)设
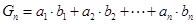 ,求
,求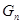 .
.(1)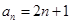 (2)
(2)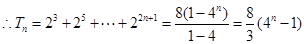 (3)
(3)
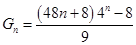
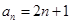 (2)
(2)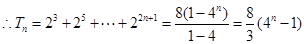 (3)
(3)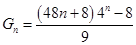
(1)考查数列中
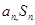 之间的关系,
之间的关系,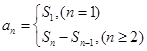 ,可解得
,可解得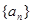 的通项公式;(2)再据
的通项公式;(2)再据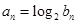 可求得数列
可求得数列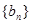 的通项公式,进而求证
的通项公式,进而求证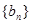 是等比数列;
是等比数列;(3)
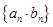 是差比数列,根据错位想减法求和,
是差比数列,根据错位想减法求和,
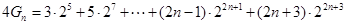
注意想减时相同次数的想减,最后一项注意符号的变化,再用等比数列的求和方式求和。
解:(1)∵
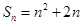
∴当
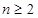 时,
时,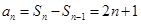 ;当
;当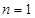 时,
时,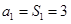 ,也满足上式,
,也满足上式,∴综上得
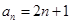 ………………5分
………………5分(2)由
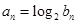 得
得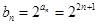 ,
,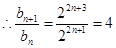 ,
,  数列
数列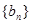 是等比数列,其中
是等比数列,其中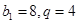
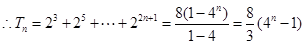 ……………10分
……………10分(3)

∴
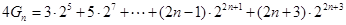
两式相减得:
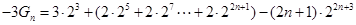
即:
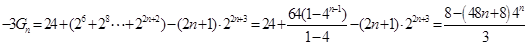
∴
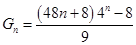

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的前n项和
的前n项和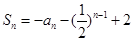 (n为正整数)。
(n为正整数)。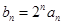 ,求证数列
,求证数列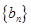 是等差数列,
是等差数列,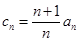 ,
,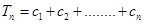 。是否存在最小的正整数
。是否存在最小的正整数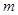 ,使得对于
,使得对于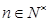 都有
都有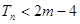 恒成立,若存在,求出
恒成立,若存在,求出 中,
中,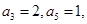 如果数列
如果数列 是等差数列,则
是等差数列,则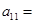 ( )
( )
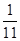
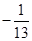

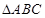 的三个内角
的三个内角 成等差数列,且
成等差数列,且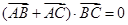 ,则
,则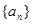 的通项公式是
的通项公式是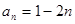 ,其前
,其前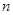 项和为
项和为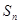 ,则数列
,则数列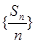 的前11项和为( )
的前11项和为( )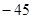
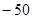
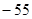
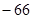
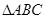 中角
中角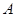 、
、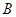 、
、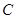 成等差数列,则
成等差数列,则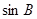 =( )
=( )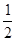
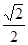
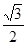
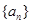 中,
中,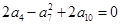 ,则
,则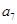 的值为( )
的值为( )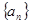 中,如果存在正整数
中,如果存在正整数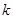 和
和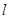 (
(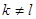 ),使得前
),使得前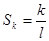 ,前
,前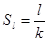 ,则( )
,则( )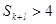
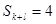
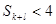
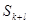 与4的大小关系不确定
与4的大小关系不确定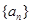 中,
中,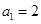 ,
, 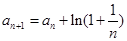 ,则
,则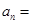 ( )
( )