题目内容
某人骑自行车上班，第一条路线较短但拥挤，到达时间X(分钟)服从正态分布N(5,1);第二条路较长不拥挤，X服从N(6,0.16).有一天她出发时离点名时间还有7分钟，问他应选哪一条路线？若离点名时间还有6.5分钟，问他应选哪一条路线？
见解析
解：还有7分钟时，若选第一条线，X服从N(5,1)，能及时到达的概率
P1=P(X≤7)=P(X≤5)+ P(5<X<7)=
+
若选第二条线，X服从N(6,0.16)，能及时到达的概率
P2=P(X≤7)=P(X≤6)+ P(6<X<7)=+
所以P1〈P2，选第二条路.同理，还有6.5分钟时，选第一条路.
P1=P(X≤7)=P(X≤5)+ P(5<X<7)=
+若选第二条线，X服从N(6,0.16)，能及时到达的概率
P2=P(X≤7)=P(X≤6)+ P(6<X<7)=
+所以P1〈P2，选第二条路.同理，还有6.5分钟时，选第一条路.
练习册系列答案
相关题目
·
(x∈R).
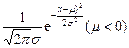的图象为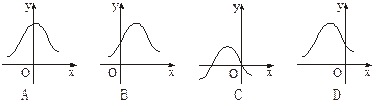
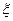～N（175，6
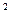）单位：cm，车门应设计的高度至少为 。
）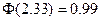