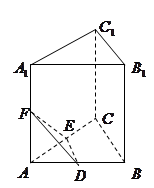题目内容
如图,斜三棱柱ABC-A'B'C'中,底面是边长为a的正三角形,侧棱长为b,侧棱AA'与底面相邻两边AB,AC都成45°角.

(Ⅰ)求此斜三棱柱的表面积.
(Ⅱ)求三棱锥B'-ABC的体积.

(Ⅰ)求此斜三棱柱的表面积.
(Ⅱ)求三棱锥B'-ABC的体积.
(1)(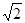 +1)ab+
+1)ab+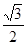 a2;(2)
a2;(2)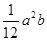 .
.
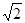 +1)ab+
+1)ab+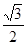 a2;(2)
a2;(2)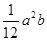 .
.试题分析:(1)要求表面积,最难求的是面
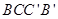 的面积,要分析它的特征,如图,过A'作A'D⊥平面ABC于点D,过点D作DE⊥AB于点E,DF⊥AC于点F,连接A'E,A'F,AD.由题意可知∠A'AE=∠A'AF=45°,AA'=AA',于是Rt△A'AE≌Rt△A'AF.,因此A'E=A'F,从而可得DE=DF.故AD平分∠BAC,又∵AB=AC,∴BC⊥AD.故BC⊥AA'.∵AA'∥BB',∴BC⊥BB'.因此四边形BCC'B'是矩形,故斜三棱柱的侧面积为2×a×bsin45°+ab=(
的面积,要分析它的特征,如图,过A'作A'D⊥平面ABC于点D,过点D作DE⊥AB于点E,DF⊥AC于点F,连接A'E,A'F,AD.由题意可知∠A'AE=∠A'AF=45°,AA'=AA',于是Rt△A'AE≌Rt△A'AF.,因此A'E=A'F,从而可得DE=DF.故AD平分∠BAC,又∵AB=AC,∴BC⊥AD.故BC⊥AA'.∵AA'∥BB',∴BC⊥BB'.因此四边形BCC'B'是矩形,故斜三棱柱的侧面积为2×a×bsin45°+ab=(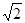 +1)ab.又∵斜三棱柱的底面积为2×
+1)ab.又∵斜三棱柱的底面积为2×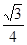 a2=
a2=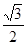 a2,∴斜三棱柱的表面积为(
a2,∴斜三棱柱的表面积为(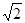 +1)ab+
+1)ab+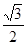 a2.(2)求B'-ABC的体积,要求出底面ABC的面积
a2.(2)求B'-ABC的体积,要求出底面ABC的面积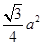 ,高
,高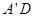 的求解根据
的求解根据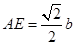 ,
,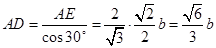 ,
,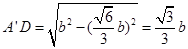 ,
,所以
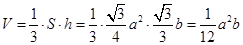 .
.试题解析:
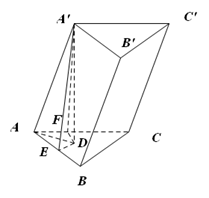
(1)如图,过A'作A'D⊥平面ABC于点D,过点D作DE⊥AB于点E,DF⊥AC于点F,连接A'E,A'F,AD.
由题意可知∠A'AE=∠A'AF=45°,AA'=AA',于是Rt△A'AE≌Rt△A'AF.
因此A'E=A'F,从而可得DE=DF.故AD平分∠BAC,
又∵AB=AC,∴BC⊥AD.故BC⊥AA'.∵AA'∥BB',∴BC⊥BB'.因此四边形BCC'B'是矩形,故斜三棱柱的侧面积为2×a×bsin45°+ab=(
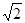 +1)ab.
+1)ab.又∵斜三棱柱的底面积为2×
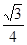 a2=
a2=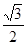 a2,∴斜三棱柱的表面积为(
a2,∴斜三棱柱的表面积为(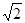 +1)ab+
+1)ab+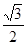 a2.
a2.(2)由(1)
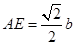 ,
,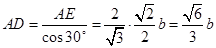 ,
,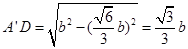 ,所以
,所以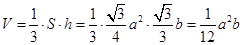 .
.
练习册系列答案
相关题目
 的底面是正方形,
的底面是正方形, 底面
底面 ,
,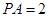 ,
,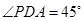 ,点
,点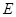 、
、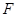 分别为棱
分别为棱 、
、 的中点.
的中点.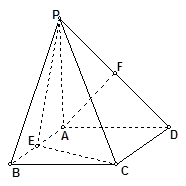
 平面
平面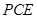 ;
;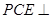 平面
平面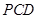 ;
;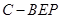 的体积.
的体积. 中,
中, 是边长为
是边长为 的正三角形,平面
的正三角形,平面 ⊥平面
⊥平面 ,
, ,
, 、
、 分别为
分别为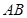 、
、 的中点.
的中点.
 ⊥
⊥ 的体积.
的体积. 
 是边长为2的正方形,
是边长为2的正方形,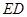 ⊥平面
⊥平面 ,
,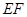 //
// 且
且 .
.
 ⊥平面
⊥平面 ;
; 的体积.
的体积.  种侧棱垂直于底面,
种侧棱垂直于底面, ,
, ,
, ,且三棱柱
,且三棱柱 的面对角线
的面对角线 上存在一点P使得
上存在一点P使得 最短,则
最短,则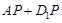 的最小值 .
的最小值 . 绕直线
绕直线 旋转一周所得的几何体的体积为( )
旋转一周所得的几何体的体积为( )



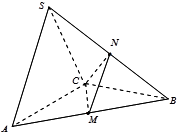
 中,
中, 分别是
分别是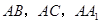 的中点,设三棱锥
的中点,设三棱锥 的体积为
的体积为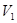 ,三棱柱
,三棱柱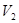 ,则
,则 .
.