题目内容
数列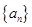 的前n项和记为
的前n项和记为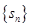 ,已知
,已知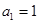 ,
,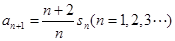 .
.
证明:(1)数列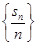 是等比数列;
是等比数列;
(2)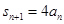 .
.
(1)由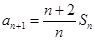 ,
,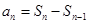 得
得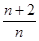 Sn=Sn+1-Sn,∴Sn+1=
Sn=Sn+1-Sn,∴Sn+1=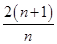 Sn,∴
Sn,∴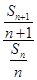 =2
=2
∴数列{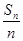 }为等比数列(2)由⑴知{
}为等比数列(2)由⑴知{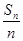 }公比为2∴
}公比为2∴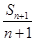 =
=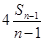 =
=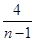 ·
·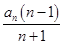 ∴Sn+1=4an
∴Sn+1=4an
解析试题分析:⑴由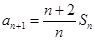 ,
,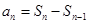 得
得
∴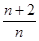 Sn=Sn+1-Sn, 2分
Sn=Sn+1-Sn, 2分
∴Sn+1=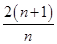 Sn,
Sn,
∴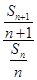 =2, 4分
=2, 4分
∴数列{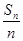 }为等比数列. 6分
}为等比数列. 6分
⑵由⑴知{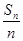 }公比为2, 8分
}公比为2, 8分
∴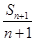 =
=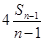 =
=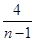 ·
·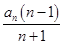 , 10分
, 10分
∴Sn+1=4an. 12分
考点:等比数列及求和
点评:要证明一数列是等比数列需用定义,如要证明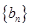 是等比数列只需证明
是等比数列只需证明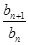 是常数,另本题中用到了关系式
是常数,另本题中用到了关系式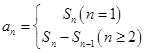

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
数列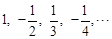 的一个通项公式为( )
的一个通项公式为( )
A.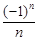 | B.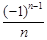 | C.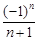 | D.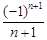 |
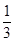 )是函数
)是函数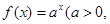 且
且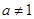 )的图象上一点,等比数列
)的图象上一点,等比数列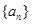 的前
的前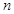 项和为
项和为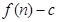 ,数列
,数列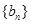
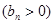 的首项为
的首项为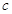 ,且前
,且前 满足
满足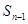 =
=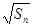 +
+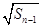 (
( ).
).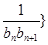 前
前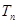 .
.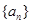 的前n项和为
的前n项和为 ,已知
,已知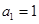 ,
,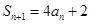
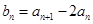 ,证明数列
,证明数列 是等比数列 (2)求数列
是等比数列 (2)求数列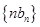 的前
的前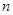 项和
项和
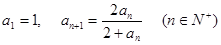 ,试猜想这个数列的通项公式。
,试猜想这个数列的通项公式。 }满足a
}满足a =2a
=2a +a
+a ,且a
,且a +a
+a =2a
=2a +4,其中n∈N
+4,其中n∈N .
. ,求数列{b
,求数列{b +
+ +…+
+…+ >
> (n≥2).
(n≥2).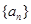 中,
中,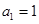 ,
,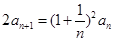 .
. ,求数列
,求数列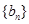 的前
的前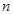 项和
项和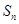 .
. 的各项均为正数,且满足
的各项均为正数,且满足 ,
,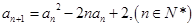 .
. 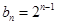 ,令
,令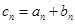 ,求数列
,求数列 的前
的前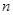 项和
项和
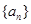 中,
中,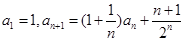 ,
, 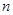 项和
项和