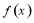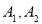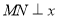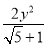题目内容
数列{an}(n∈N﹡)中,a1=0,当3an<n2时,an+1=n2,当3an>n2时,an+1=3an.求a2,a3,a4,a5,猜测数列的通项an并证明你的结论.
 .
.
【解析】
试题分析:先由递推公式分别求出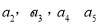 的值,猜测数列的通项
的值,猜测数列的通项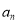 ,再用数学归纳法证明即可.
,再用数学归纳法证明即可.
试题解析:当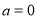 时,
时,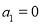 ,则
,则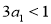 ,知
,知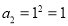 ,因为
,因为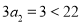 ,由数列
,由数列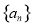 定义知
定义知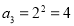 .因为
.因为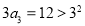 ,由数列定义知
,由数列定义知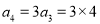 .又因为
.又因为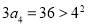 ,由定义知
,由定义知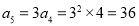
4分
由此猜测:当n≥3时,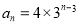 6分
6分
下面用数学归纳法去证明:当n≥3时,3an>n2.当n=3时,由前面的讨论知结论成立.假设当n=k(k≥3)时,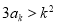 成立.则由数列
成立.则由数列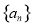 定义知
定义知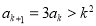 ,从而
,从而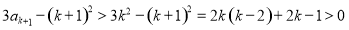 .所以
.所以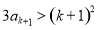 ,即当n=k+1(k≥3)时,
,即当n=k+1(k≥3)时,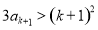 成立. 故当n≥3时,
成立. 故当n≥3时,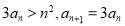 .而
.而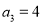 .因此
.因此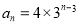 . 11分
. 11分
综上所述,当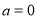 时,
时,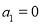 ,
,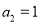 ,
,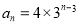 ( n≥3) 13分
( n≥3) 13分
考点:推理与证明、数学归纳法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目