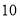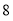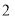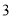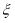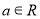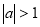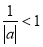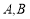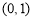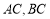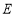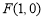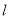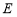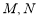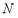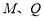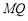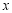Question

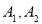我们把离心率为e＝的双曲线(a>0，b>0)称为黄金双曲线．如图，是双曲线的实轴顶点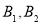，是虚轴的顶点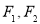，是左右焦点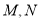，在双曲线上且过右焦点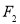，并且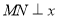轴，给出以下几个说法：

①双曲线x2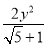－＝1是黄金双曲线；

②若b2＝ac，则该双曲线是黄金双曲线；

③如图，若∠F1B1A2＝90°，则该双曲线是黄金双曲线；

④如图，若∠MON＝90°，则该双曲线是黄金双曲线．

其中正确的是(　　)

A．①②④ B．①②③ C．②③④ D．①②③④

 

Answer 1

D

【解析】

试题分析：①由双曲线x2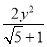－＝1，可得离心率e=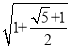，即可判断出该双曲线是否是黄金双曲线；

②由b2=ac，可得c2-a2-ac=0，化为e2-e-1=0，又e＞1，解得e，即可判断出该双曲线是否是黄金双曲线；

③如图，由∠F1B1A2=90°，可得|B1F1|2+|B1A2|2＝|F1A2|2，可得b2+c2+b2+a2=（a+c）2，化为c2-ac-a2=0，即可判断出该双曲线是否是黄金双曲线；

④如图，由∠MON=90°，可得MN⊥x轴，|MF2|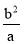＝，可得△MOF2是等腰直角三角形，得到c=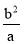，即可判断出该双曲线是否是黄金双曲线．

考点：圆锥曲线的综合应用.