题目内容
【题目】某化工厂生产甲、乙两种混合肥料，需要A，B，C三种主要原料，生产1扯皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如表所示：
配料 原料 | A | B | C |
甲 | 4 | 8 | 3 |
乙 | 5 | 5 | 10 |
现有A种原料200吨，B种原料360吨，C种原料300吨，在此基础上生产甲、乙两种肥料．已知生产1车皮甲种肥料，产生的利润为2万元；生产1车品乙种肥料，产生的利润为3万元、分别用x，y表示计划生产甲、乙两种肥料的车皮数．
（1）用x，y列出满足生产条件的数学关系式，并画出相应的平面区域；
（2）问分别生产甲、乙两种肥料，求出此最大利润．
【答案】
（1）
解：x，y满足的条件关系式为：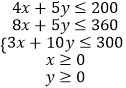 
．
作出平面区域如图所示：
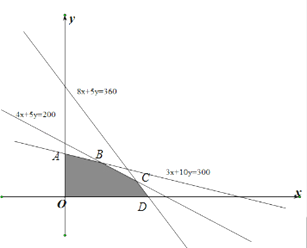
（2）
解：设利润为z万元，则z=2x+3y．
∴y=﹣ 
x+ 
．
∴当直线y=﹣ x+ 经过点B时，截距 最大，即z最大．
解方程组 
得B（20，24）．
∴z的最大值为2×20+3×24=112．
答：当生产甲种肥料20吨，乙种肥料24吨时，利润最大，最大利润为112万元
【解析】（1）根据原料的吨数列出不等式组，作出平面区域；（2）令利润z=2x+3y，则y=﹣ 
，结合可行域找出最优解的位置，列方程组解出最优解．；本题考查了简单的线性规划的应用，抽象概括能力和计算求解能力，属于中档题．
【题目】某险种的基本保费为a（单位：元），继续购买该险种的投保人称为续保人，续保人的本年度的保费与其上年度的出险次数的关联如下：
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
设该险种一续保人一年内出险次数与相应概率如下：
一年内出险次数 | 0 | 1 | 2 | 3 | 4 |
|
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0. 05 |
（1）求一续保人本年度的保费高于基本保费的概率；
（2）若一续保人本年度的保费高于基本保费，求其保费比基本保费高出60%的概率；
（3）求续保人本年度的平均保费与基本保费的比值.
【题目】某车间为了规定工时定额，需确定加工零件所花费的时间，为此做了4次试验，得到的数据如下：
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 | 2.5 | 3 | 4 | 4.5 |
若加工时间
与零件个数
之间有较好的相关关系．
（1）求加工时间与零件个数的线性回归方程
．
（2）试预报加工10个零件需要的时间．
附录：参考公式：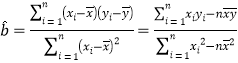
，
.
