题目内容
(本小题满分13分)已知函数f
(x) = 
(1)若函数f (x)在其定义域内为单调函数,求实数a的取值范围;
(2)若函数f (x)的图象在x = 1处的切线垂直于y轴,数列{ }满足
}满足
 .
.
①若a1≥3,求证:an≥n + 2 ;
;
②若a1 = 4,试比较 的大小,并说明你的理由.
的大小,并说明你的理由.
①a≥1或a≤0.②<
【解析】(1)∵f (1) =
a – b = 0,∴a = b,∴f′(x) = 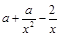 .要使函数f (x)在其定义域内为单调函数,则
.要使函数f (x)在其定义域内为单调函数,则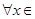 (0,+∞)内
(0,+∞)内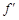 (x) =
(x) = 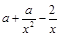 恒大于等于零,或恒小于等于零.
恒大于等于零,或恒小于等于零.
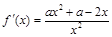 由
由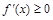 得
得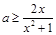 而
而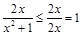
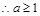 由
由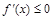 得
得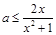 而
而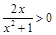
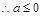 经验证a=0及a=1均合题意,故
经验证a=0及a=1均合题意,故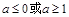
∴所求实数a的取值范围为a≥1或a≤0. ………………………5分
(2)∵函数f (x)的图象在x = 1处的切线的斜率为0,∴f′(1) = 0,即a + a – 2 = 0,解得a = 1,∴f′(x) = 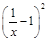 ,∴an + 1 = f′
,∴an + 1 = f′ ……7分
……7分
①用数学归纳法证明:(i)当n
= 1时,a1≥3 = 1 + 2,不等式成立;(ii)假设当n = k时不等式成立,即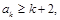 那么ak – k≥2>0,∴ak + 1 = ak (ak – k) + 1≥2 (k + 2) + 1 = (k
+ 3) + k + 2>k + 3,也就是说,当n
那么ak – k≥2>0,∴ak + 1 = ak (ak – k) + 1≥2 (k + 2) + 1 = (k
+ 3) + k + 2>k + 3,也就是说,当n = k + 1时,ak + 1≥(k + 1) + 2.根据(i)和(ii),对于所有n≥1,有an≥n + 2.
……………………………………10分
= k + 1时,ak + 1≥(k + 1) + 2.根据(i)和(ii),对于所有n≥1,有an≥n + 2.
……………………………………10分
②由an + 1 = an (an – n) + 1及①,对k≥2,有ak = ak – 1 (ak–1
– k + 1) + 1≥ak –1 (k – 1 + 2 – k + 1) + 1 = 2ak–1 + 1,∴ak + 1≥2 (ak–1 + 1)≥22
(ak – 2 + 1)≥23 (ak –3 + 1)≥…≥2k–1
(a1 + 1) 而
而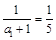 ,于是当k≥2时,
,于是当k≥2时,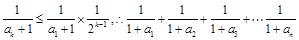
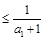
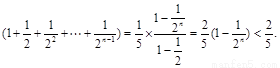 …………………………13分
…………………………13分

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
 .
. 的最小正周期和最大值;
的最小正周期和最大值; 在区间
在区间 上的图象.
上的图象. ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围. 的函数
的函数 是奇函数.
是奇函数. 的值;(2)判断函数
的值;(2)判断函数 的单调性;
的单调性; ,不等式恒成立
,不等式恒成立 ,求k的取值范围.
,求k的取值范围. ,
,  ,
, .
. (∁
(∁ ; (2)若
; (2)若 ,求
,求 的取值范围.
的取值范围. 的所有棱长都为2,
的所有棱长都为2, 为
为 的中点。
的中点。 ∥平面
∥平面 ;
; 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
. 的表达式;
的表达式; 中,若
中,若 A=2
A=2 ,BC=2,求
,BC=2,求 的前
的前 项和
项和