题目内容
(本题满分16分)
设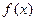 是定义在R上的奇函数,且对任意a、b
是定义在R上的奇函数,且对任意a、b ,当
,当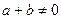 时,都有
时,都有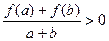 .
.
(1)若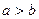 ,试比较
,试比较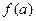 与
与 的大小关系;
的大小关系;
(2)若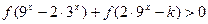 对任意
对任意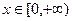 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
(1)因为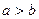 ,所以
,所以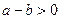 ,由题意得:
,由题意得: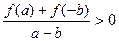 ,所以
,所以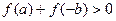 ,又
,又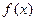 是定义在R上的奇函数,
是定义在R上的奇函数,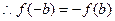
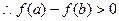 ,即
,即 .
.
(2)由(1)知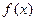 为R上的单调递增函数,
为R上的单调递增函数, 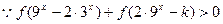 对任意
对任意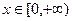 恒成立,
恒成立,  ,即
,即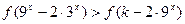 ,
, 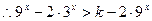 ,
,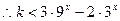 对任意
对任意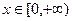 恒成立,
恒成立,
即k小于函数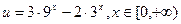 的最小值.
的最小值.
令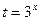 ,则
,则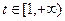
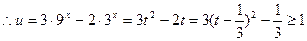 ,
,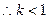 .
.
解析

练习册系列答案
相关题目
 成本)
成本) 满足:①定义域是
满足:①定义域是 ; ②当
; ②当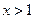 时,
时,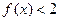 ;
;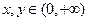 ,总有
,总有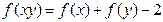
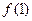 的值;
的值;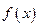 对任意的
对任意的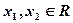 ,都有
,都有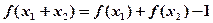 成立,且当
成立,且当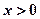 时,
时, 。
。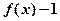 为奇函数; (2)求证:
为奇函数; (2)求证: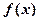 是R上的增函数;
是R上的增函数;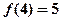 ,解不等式
,解不等式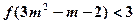 .
.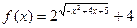 .
. 的定义域;
的定义域;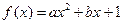 (
( 为实数,
为实数, ,
,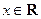 ).
). 的图像过点
的图像过点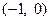 ,且方程
,且方程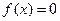 有且只有一个根,求
有且只有一个根,求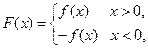 当
当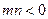 ,
,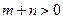 ,
,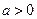 ,且函数
,且函数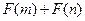 能否大于
能否大于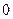 ?
? ) .已知函数y=
) .已知函数y=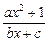 (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<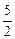
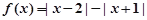 .
.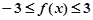 ;
;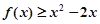 .
.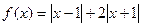
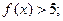
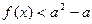 的解集为空集,求
的解集为空集,求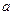 的取值范围.
的取值范围.