题目内容
已知,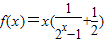 ,
,(1)求f(x)的定义域
(2)判断f(x)的奇偶性,并说明理由;
(3)证明f(x)>0.
【答案】分析:(1)由2x-1≠0即可求得f(x)的定义域;
(2)利用奇偶函数的定义f(-x)=-f(x)或f(-x)=f(x)即可判断f(x)的奇偶性;
(3)可对x分x>0与x<0讨论解决.
解答:解:(1)由2x-1≠0得x≠0,
∴f(x)的定义域为{x|x≠0,x∈R}.
(2)∵f(x)=x(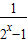 +
+ )=
)=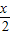 •
•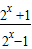 ,
,
f(-x)=-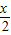 •
•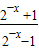 =
=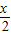 •
•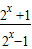 =f(x),
=f(x),
∴f(x)为偶函数.
(3)证明:∵f(x)=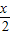 •
•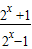 ,
,
当x>0,2x>2,即2x-1>0,又2x+1>0,
∴f(x)>0;
同理当x<0,则2x-1<0,又2x+1>0,
∴f(x)=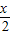 •
•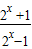 >0;
>0;
∴f(x)>0.
又x≠0.综上所述,f(x)>0.
点评:本题考查函数奇偶性的判断,着重综合考查函数的性质,属于中档题.
(2)利用奇偶函数的定义f(-x)=-f(x)或f(-x)=f(x)即可判断f(x)的奇偶性;
(3)可对x分x>0与x<0讨论解决.
解答:解:(1)由2x-1≠0得x≠0,
∴f(x)的定义域为{x|x≠0,x∈R}.
(2)∵f(x)=x(
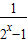 +
+ )=
)=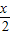 •
•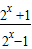 ,
,f(-x)=-
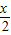 •
•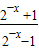 =
=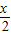 •
•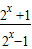 =f(x),
=f(x),∴f(x)为偶函数.
(3)证明:∵f(x)=
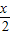 •
•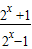 ,
,当x>0,2x>2,即2x-1>0,又2x+1>0,
∴f(x)>0;
同理当x<0,则2x-1<0,又2x+1>0,
∴f(x)=
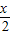 •
•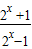 >0;
>0;∴f(x)>0.
又x≠0.综上所述,f(x)>0.
点评:本题考查函数奇偶性的判断,着重综合考查函数的性质,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
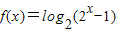 ,
,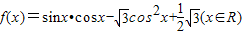 ,
,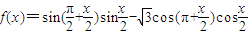 .
.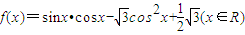 ,
,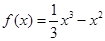 .
.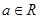 ,设函数
,设函数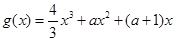 的单调递减区间为
的单调递减区间为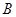 ,且
,且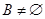 ,
,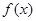 的单调递减区间为
的单调递减区间为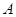 ,若
,若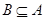 ,求
,求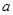 的取值范围.
的取值范围.