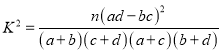题目内容
【题目】选修4-4：坐标系与参数方程
在直角坐标系
中，曲线
的参数方程为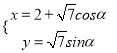
（其中
为参数），曲线
： 
，以坐标原点
为极点， 
轴的正半轴为极轴建立极坐标系.
（1）求曲线
的普通方程和曲线
的极坐标方程；
（2）若射线
（
）与曲线
， 
分别交于
， 
两点，求
.
【答案】（1）曲线
的普通方程为
；曲线
的极坐标方程
（2）
的最小值为3
【解析】试题分析：（1）利用平方法消去参数可求曲线
的普通方程， 
利用
即可得结果曲线
的极坐标方程；（2）将
代入曲线
的极坐标方程得
，解得
，同理将
曲线
的极坐标方程得
，可得
.
试题解析：（1）由
，有曲线
的普通方程为
.
把
， 
，代入
得
，
化简得，曲线
的极坐标方程
.
（2）依题意可设
.
因为曲线
的极坐标方程为
，
将
（
）代入曲线
的极坐标方程得
，解得
.
同理将
（
）曲线
的极坐标方程得
，所以
.
【题目】“DD共享单车”是为城市人群提供便捷经济、绿色低碳的环保出行方式，根据目前在三明市的投放量与使用的情况，有人作了抽样调查，抽取年龄在二十至五十岁的不同性别的骑行者，统计数据如下表所示：
男性 | 女性 | 合计 | |
20～35岁 |
| 40 | 100 |
36～50岁 | 40 |
| 90 |
合计 | 100 | 90 | 190 |
(1)求统计数据表中
的值；
(2)假设用抽到的100名20～35岁年龄的骑行者作为样本估计全市的该年龄段男女使用“DD共享单车”情况，现从全市的该年龄段骑行者中随机抽取3人，求恰有一名女性的概率；
(3)根据以上列联表，判断使用“DD共享单车”的人群中，能否有
的把握认为“性别”与“年龄”有关，并说明理由.
参考数表：
|
|
|
|
|
|
|
|
|
|
参考公式：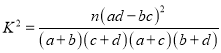 
， 
.
【题目】为了弘扬民族文化，某校举行了“我爱国学，传诵经典”考试，并从中随机抽取了100名考生的成绩（得分均为整数,满足100分）进行统计制表，其中成绩不低于80分的考生被评为优秀生，请根据频率分布表中所提供的数据，用频率估计概率，回答下列问题.
分组 | 频数 | 频率 |
| 5 | 0.05 |
|
| 0.20 |
| 35 |
|
| 25 | 0.25 |
| 15 | 0.15 |
合计 | 100 | 1.00 |
（1）求
的值并估计这100名考生成绩的平均分；
（2）按频率分布表中的成绩分组，采用分层抽样抽取20人参加学校的“我爱国学”宣传活动，求其中优秀生的人数；
