题目内容
【题目】对于函数f1(x),f2(x),h(x),如果存在实数a,b使得h(x)=af1(x)+bf2(x),那么称h(x)为f1(x),f2(x)的生成函数.
(1)函数f1(x)=x2﹣x,f2(x)=x2+x+1,h(x)=x2﹣x+1,h(x)是否为f1(x),f2(x)的生成函数?说明理由;
(2)设f1(x)=1﹣x,f2(x)=![]() ,当a=b=1时生成函数h(x),求h(x)的对称中心(不必证明);
,当a=b=1时生成函数h(x),求h(x)的对称中心(不必证明);
(3)设f1(x)=x,![]() (x≥2),取a=2,b>0,生成函数h(x),若函数h(x)的最小值是5,求实数b的值.
(x≥2),取a=2,b>0,生成函数h(x),若函数h(x)的最小值是5,求实数b的值.
【答案】(1)不是,理由见解析;(2)(1,1);(3)1
【解析】
(1)先假设存在,列出方程,根据方程无解,得出不存在;
(2)化简函数式为h(x)=1﹣x+![]()
![]() +1,从而判断函数图象关于点(1,1)中心对称;
+1,从而判断函数图象关于点(1,1)中心对称;
(3)运用双勾函数的图象和性质,并通过分类讨论确定函数的最值.
解:(1)根据生成函数的定义,设存在a,b使得h(x)=af1(x)+bf2(x),
则x2﹣x+1=a(x2﹣x)+b(x2+x+1)=(a+b)x2+(b﹣a)x+b,
对比两边的系数可知,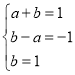 ,方程无解,
,方程无解,
所以,h(x)不是f1(x),f2(x)的生成函数;
(2)因为a=b=1,所以,h(x)=1﹣x+![]() ,
,
而h(x)=1﹣x+![]() =(1﹣x)+
=(1﹣x)+![]() =
=![]() +1,
+1,
该函数的图象为双曲线,对称中心为(1,1);
(3)根据题意,h(x)=2x+![]() =2(x﹣1)+
=2(x﹣1)+![]() +2(x≥2),
+2(x≥2),
根据基本不等式,2(x﹣1)+![]() ≥2
≥2![]() ,
,
当且仅当:x=![]() +1时,取“=”,
+1时,取“=”,
因此,函数h(x)在(1,![]() +1)上单调递减,在(
+1)上单调递减,在(![]() +1,+∞)上单调递增,
+1,+∞)上单调递增,
故令![]() +1=2,解得b=2,最值情况分类讨论如下:
+1=2,解得b=2,最值情况分类讨论如下:
①当b∈(0,2]时,![]() +1≤2,
+1≤2,
所以,当x≥2/span>时,h(x)单调递增,h(x)min=h(2)=b+4=5,解得b=1,符合题意;
②当b∈(2,+∞)时,![]() +1>2,
+1>2,
所以,当x≥2时,h(x)先减后增,h(x)min=h(![]() +1)=2
+1)=2![]() +2=5,解得b=
+2=5,解得b=![]() ,不合题意;
,不合题意;
综上:实数b的值为1.

 名校课堂系列答案
名校课堂系列答案【题目】某公司为了了解一年内的用水情况,抽取了10天的用水量如下表所示:
天数 | 1 | 1 | 1 | 2 | 2 | 1 | 2 |
用水量/吨 | 22 | 38 | 40 | 41 | 44 | 50 | 95 |
(Ⅰ)在这10天中,该公司用水量的平均数是多少?每天用水量的中位数是多少?
(Ⅱ)你认为应该用平均数和中位数中的哪一个数来描述该公司每天的用水量?
【题目】社会在对全日制高中的教学水平进行评价时,常常将被清华北大录取的学生人数作为衡量的标准之一.重庆市教委调研了某中学近五年(2013年-2017年)高考被清华北大录取的学生人数,制作了如下所示的表格(设2013年为第一年).
年份(第 |
|
|
|
|
|
人数( |
|
|
|
|
|
(1)试求人数![]() 关于年份
关于年份![]() 的回归直线方程
的回归直线方程![]() ;
;
(2)在满足(1)的前提之下,估计2018年该中学被清华北大录取的人数(精确到个位);
(3)教委准备在这五年的数据中任意选取两年作进一步研究,求被选取的两年恰好不相邻的概率.
参考公式: .
.
【题目】某小组为了研究昼夜温差对一种稻谷种子发芽情况的影响,他们分别记录了4月1日至4月5日的每天星夜温差与实验室每天每100颗种子的发芽数,得到如下资料:
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
温差 | 9 | 10 | 11 | 8 | 12 |
发芽数 | 38 | 30 | 24 | 41 | 17 |
利用散点图,可知![]() 线性相关。
线性相关。
(1)求出![]() 关于
关于![]() 的线性回归方程,若4月6日星夜温差
的线性回归方程,若4月6日星夜温差![]() ,请根据你求得的线性同归方程预测4月6日这一天实验室每100颗种子中发芽颗数;
,请根据你求得的线性同归方程预测4月6日这一天实验室每100颗种子中发芽颗数;
(2)若从4月1日![]() 4月5日的五组实验数据中选取2组数据,求这两组恰好是不相邻两天数据的概率.
4月5日的五组实验数据中选取2组数据,求这两组恰好是不相邻两天数据的概率.
(公式: )
)

